二項分布の確率母関数を求め、期待値と分散を算出しました。
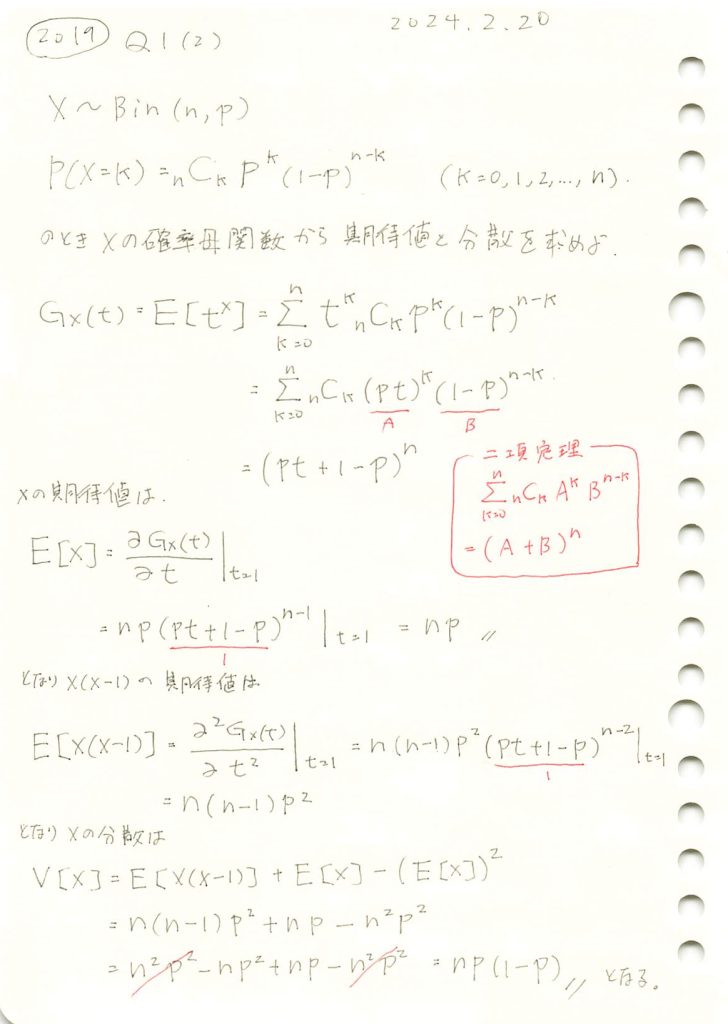
コード
非負の離散型観測データから確率母関数を構築し、これの微分と2階微分から期待値と分散を求めます。ここでは、観測データとして二項分布の乱数を用いて、その理論的な母関数と期待値と分散の比較を行います。
# 2019 Q1(2) 2024.9.10
import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative
# パラメータ設定
n = 10 # 試行回数
p = 0.5 # 成功確率
sample_size = 10000 # サンプル数
# 1. 二項分布に従う乱数データを生成
samples = np.random.binomial(n, p, sample_size)
# 2. P(X=k) の推定(サンプル度数から確率質量関数の推定)
max_k = np.max(samples)
pmf_estimate = np.zeros(max_k + 1)
for k in range(max_k + 1):
pmf_estimate[k] = np.sum(samples == k) / sample_size
# 3. G_X(t) の推定
def G_X(t):
return np.sum([pmf_estimate[k] * t**k for k in range(max_k + 1)])
# 4. 理論的な G_X(t) (二項分布の確率母関数)
def G_X_theoretical(t, n, p):
return (p * t + (1 - p))**n
# 5. G_X(t) のプロット
t_values = np.linspace(0, 1, 100)
G_X_values = [G_X(t) for t in t_values]
G_X_theoretical_values = [G_X_theoretical(t, n, p) for t in t_values]
plt.plot(t_values, G_X_values, label="推定された G_X(t)", color="blue")
plt.plot(t_values, G_X_theoretical_values, label="理論的な G_X(t)", linestyle='--', color="red")
plt.title("推定された確率母関数と理論的な G_X(t) の比較")
plt.xlabel("t")
plt.ylabel("G_X(t)")
plt.legend()
plt.show()
# 6. G_X(t) の微分と2階微分
def G_X_diff_1(t):
return derivative(G_X, t, dx=1e-6)
def G_X_diff_2(t):
return derivative(G_X_diff_1, t, dx=1e-6)
# 7. t = 1 における期待値と分散の推定
E_X_estimated = G_X_diff_1(1) # 期待値
Var_X_estimated = G_X_diff_2(1) + E_X_estimated - E_X_estimated**2 # 分散
# 結果の出力
print(f"推定された期待値 E[X]: {E_X_estimated}")
print(f"推定された分散 Var(X): {Var_X_estimated}")
# 真の期待値と分散を計算
E_X_true = n * p
Var_X_true = n * p * (1 - p)
# 真の期待値と分散を出力
print(f"真の期待値 E[X]: {E_X_true}")
print(f"真の分散 Var(X): {Var_X_true}")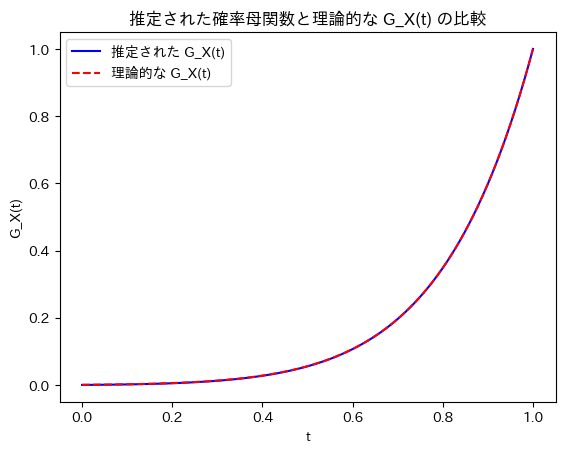
推定された期待値 E[X]: 4.9988999998862305
推定された分散 Var(X): 2.4964947096596752
真の期待値 E[X]: 5.0
真の分散 Var(X): 2.5観測値から推定された確率母関数は理論的な二項分布の確率母関数と一致しました。また、推定された確率母関数から計算された期待値と分散も、真の値に非常に近い結果となりました。
次に、二項分布の確率母関数![]() 、その1階微分
、その1階微分 ![]() 、および2階微分
、および2階微分 ![]() を視覚的に比較してみます。
を視覚的に比較してみます。
# 2019 Q1(2) 2024.9.10
import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative
# パラメータ設定
n = 10 # 試行回数
p = 0.5 # 成功確率
# 確率母関数 G_X(t)
def G_X(t, n, p):
return (p * t + (1 - p))**n
# 1階微分 G'_X(t)
def G_X_diff_1(t, n, p):
return derivative(lambda t: G_X(t, n, p), t, dx=1e-6)
# 2階微分 G''_X(t)
def G_X_diff_2(t, n, p):
return derivative(lambda t: G_X_diff_1(t, n, p), t, dx=1e-6)
# t の範囲を定義
t_values = np.linspace(0, 1, 100)
# G_X(t), G'_X(t), G''_X(t) の値を計算
G_X_values = [G_X(t, n, p) for t in t_values]
G_X_diff_1_values = [G_X_diff_1(t, n, p) for t in t_values]
G_X_diff_2_values = [G_X_diff_2(t, n, p) for t in t_values]
# グラフの描画
plt.plot(t_values, G_X_values, label="G_X(t) (確率母関数)", color="blue")
plt.plot(t_values, G_X_diff_1_values, label="G'_X(t) (1階微分)", color="green")
plt.plot(t_values, G_X_diff_2_values, label="G''_X(t) (2階微分)", color="red")
plt.title(f"G_X(t), G'_X(t), G''_X(t) の比較 (n={n}, p={p})")
plt.xlabel("t")
plt.ylabel("値")
plt.legend()
plt.grid(True)
plt.show()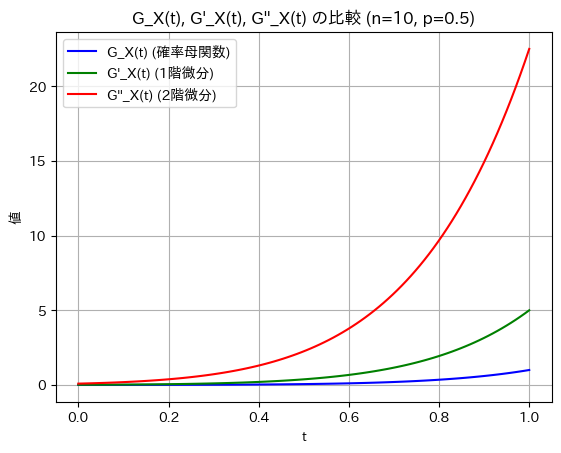
微分を重ねるごとにt=1付近での傾きが急になり大きな値を取っています。期待値や分散などの高次統計量に関連しているため、その値が大きくなっていると思います。