二項分布の期待値と条件付き期待値との比が2倍になるパラメータを求めました。

コード
n=8に固定しθを変化させて、η(θ)、E[X]、2E[X]の理論値をプロットしてみます。
# 2018 Q3(4) 2024.10.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 8 # 試行回数
theta_values = np.linspace(0.01, 0.2, 50) # θを0.01から0.2まで50点で変化
# 条件付き期待値 η(θ) と 条件なしの期待値 E[X] を計算
eta_values = n * theta_values / (1 - (1 - theta_values) ** n) # η(θ)
EX_values = n * theta_values # E[X]
# 二倍のE[X]をプロットするための値
double_EX_values = 2 * EX_values
# グラフの描画
plt.plot(theta_values, eta_values, label='条件付き期待値 η(θ)', color='blue', linestyle='-', marker='o', markersize=4)
plt.plot(theta_values, EX_values, label='条件なし期待値 E[X]', color='green', linestyle='--')
plt.plot(theta_values, double_EX_values, label='2倍の E[X]', color='red', linestyle=':')
# 二倍の関係になるθの位置を求め、プロット
intersection_index = np.argmin(np.abs(eta_values - double_EX_values))
intersection_theta = theta_values[intersection_index]
intersection_eta = eta_values[intersection_index]
plt.scatter(intersection_theta, intersection_eta, color='black', zorder=5, label=f'η(θ) = 2E[X] (θ ≈ {intersection_theta:.3f})')
# キャプションの表示
plt.xlabel("θ", fontsize=12)
plt.ylabel("期待値", fontsize=12)
plt.title("θ に対する η(θ) と E[X] の比較 (理論値)", fontsize=14)
plt.legend()
plt.grid(True)
# グラフの表示
plt.show()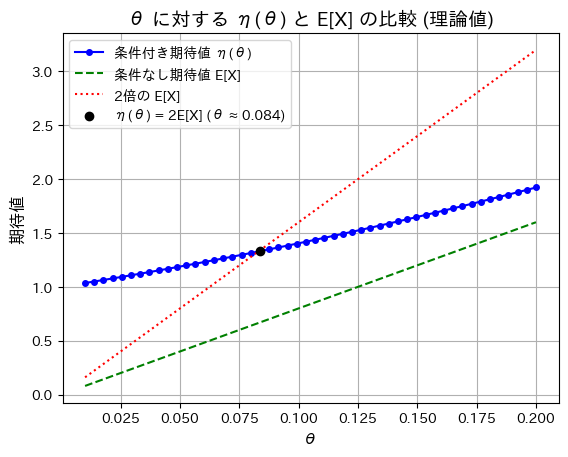
θ=0.083辺りで、η(θ)=2E[X]となることが確認できました。
次に、シミュレーションし同様に描画してみます。
# 2018 Q3(4) 2024.10.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 8 # 試行回数
theta_values = np.linspace(0.01, 0.2, 50) # θを0.01から0.2まで50点で変化
num_simulations = 100000 # シミュレーション回数
# シミュレーションによる条件付き期待値 η(θ) と 条件なし期待値 E[X] を計算
eta_values = []
EX_values = []
for theta in theta_values:
# 二項分布のサンプリング
binom_samples = np.random.binomial(n, theta, num_simulations)
# 条件付きサンプル (X >= 1)
samples_X_geq_1 = binom_samples[binom_samples >= 1]
# 条件付き期待値 η(θ)
eta = np.mean(samples_X_geq_1)
eta_values.append(eta)
# 条件なし期待値 E[X]
EX = np.mean(binom_samples)
EX_values.append(EX)
# 2倍のE[X]を計算
double_EX_values = 2 * np.array(EX_values)
# グラフの描画
plt.plot(theta_values, eta_values, label='条件付き期待値 η(θ)', color='blue', linestyle='-', marker='o', markersize=4)
plt.plot(theta_values, EX_values, label='条件なし期待値 E[X]', color='green', linestyle='--')
plt.plot(theta_values, double_EX_values, label='2倍の E[X]', color='red', linestyle=':')
# 二倍の関係になるθの位置を求め、プロット
intersection_index = np.argmin(np.abs(np.array(eta_values) - double_EX_values))
intersection_theta = theta_values[intersection_index]
intersection_eta = eta_values[intersection_index]
plt.scatter(intersection_theta, intersection_eta, color='black', zorder=5, label=f'η(θ) = 2E[X] (θ ≈ {intersection_theta:.3f})')
# キャプションの表示
plt.xlabel("θ", fontsize=12)
plt.ylabel("期待値", fontsize=12)
plt.title("θ に対する η(θ) と E[X] の比較 (シミュレーション)", fontsize=14)
plt.legend()
plt.grid(True)
# グラフの表示
plt.show()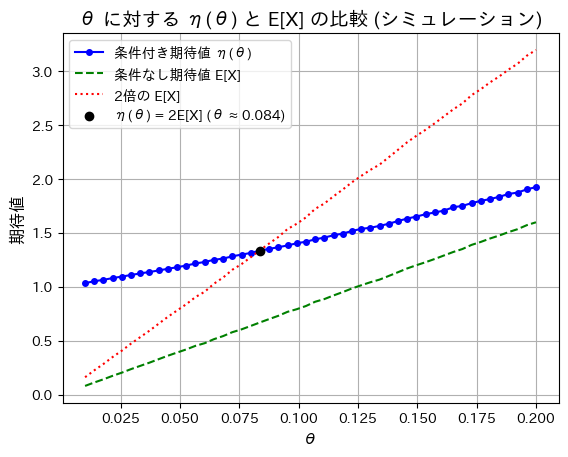
シミュレーションも同じ結果になりました。