二項分布の条件付き期待値と分散を求めました。

コード
条件付きと条件がついていない場合でシミュレーションし期待値と分散がどのように異なるのか確認します。まずn=10とします。
# 2018 Q3(3) 2024.10.15
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # 試行回数
theta = 0.5 # 成功確率
num_simulations = 100000 # シミュレーション回数
# 二項分布のサンプリング
binom_samples = np.random.binomial(n, theta, num_simulations)
# 条件 X >= 1 を満たすサンプルを抽出
samples_X_geq_1 = binom_samples[binom_samples >= 1]
# 条件付き期待値と条件付き分散のシミュレーションによる計算
simulated_mean = np.mean(samples_X_geq_1)
simulated_variance = np.var(samples_X_geq_1)
# 条件なしの期待値と分散のシミュレーションによる計算
unconditional_simulated_mean = np.mean(binom_samples)
unconditional_simulated_variance = np.var(binom_samples)
# 理論値の計算
theoretical_mean = n * theta / (1 - (1 - theta) ** n)
theoretical_variance = (
(n * theta * (1 - theta)) / (1 - (1 - theta) ** n)
- (n ** 2 * theta ** 2 * (1 - theta) ** n) / (1 - (1 - theta) ** n) ** 2
)
# 条件なしの理論期待値と分散
unconditional_theoretical_mean = n * theta
unconditional_theoretical_variance = n * theta * (1 - theta)
# 結果を表示
print(f"シミュレーションによる条件付き期待値: {simulated_mean}")
print(f"理論上の条件付き期待値: {theoretical_mean}")
print(f"シミュレーションによる条件付き分散: {simulated_variance}")
print(f"理論上の条件付き分散: {theoretical_variance}")
print(f"シミュレーションによる条件なし期待値: {unconditional_simulated_mean}")
print(f"理論上の条件なし期待値: {unconditional_theoretical_mean}")
print(f"シミュレーションによる条件なし分散: {unconditional_simulated_variance}")
print(f"理論上の条件なし分散: {unconditional_theoretical_variance}")
# ヒストグラムの描画
plt.hist(samples_X_geq_1, bins=np.arange(1, n + 2) - 0.5, density=True, alpha=0.6, color='blue', edgecolor='black', label='条件付き (X >= 1)')
plt.hist(binom_samples, bins=np.arange(0, n + 2) - 0.5, density=True, alpha=0.4, color='green', edgecolor='black', label='条件なし')
# 理論値を折れ線グラフで表示
x_values = np.arange(0, n + 1)
binom_pmf = np.array([np.math.comb(n, x) * theta**x * (1 - theta)**(n - x) for x in x_values])
conditional_pmf = binom_pmf[1:] / (1 - binom_pmf[0]) # 条件付きのPMF
plt.plot(x_values[1:], conditional_pmf, marker='x', linestyle='-', color='red', label='条件付き理論値')
plt.plot(x_values, binom_pmf, marker='o', linestyle='-', color='purple', label='条件なし理論値')
# グラフの描画
plt.xlabel("X の値", fontsize=12)
plt.ylabel("確率密度", fontsize=12)
plt.title("条件付きと条件なしの二項分布のシミュレーション", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()シミュレーションによる条件付き期待値: 5.00641686604667
理論上の条件付き期待値: 5.004887585532747
シミュレーションによる条件付き分散: 2.4896127535349235
理論上の条件付き分散: 2.4779819766102995
シミュレーションによる条件なし期待値: 5.00106
理論上の条件なし期待値: 5.0
シミュレーションによる条件なし分散: 2.5137388763999997
理論上の条件なし分散: 2.5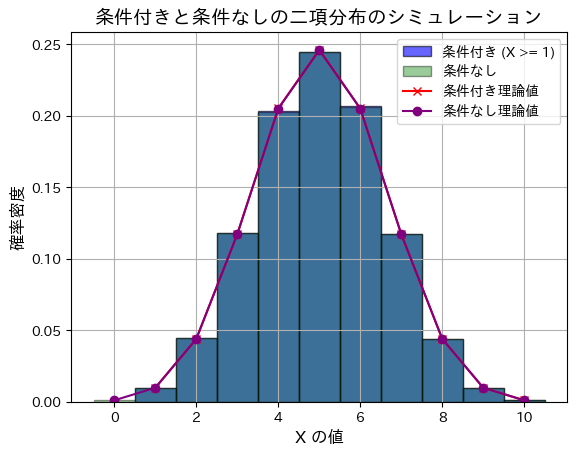
条件付きと条件がついていない場合では、分布はほとんど同じになります。
次に、n=4にすると
シミュレーションによる条件付き期待値: 2.130760208977503
理論上の条件付き期待値: 2.1333333333333333
シミュレーションによる条件付き分散: 0.7789354600394489
理論上の条件付き分散: 0.7822222222222222
シミュレーションによる条件なし期待値: 1.99844
理論上の条件なし期待値: 2.0
シミュレーションによる条件なし分散: 0.9949975664
理論上の条件なし分散: 1.0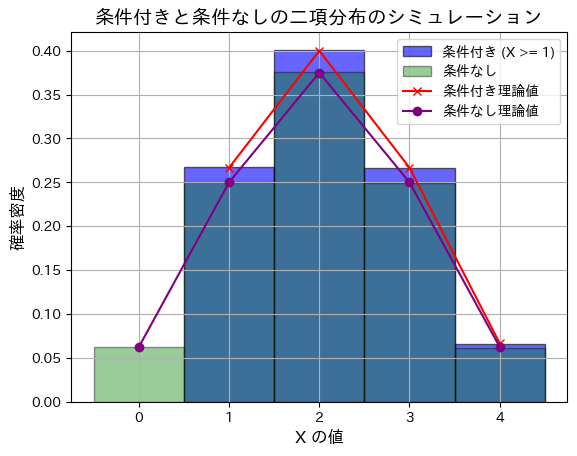
条件付きと条件がついていない場合で、分布の違いが見えてきました。
次に、n=を1から10に変化させて、条件付きと条件がついていない場合の期待値を見てみます。
# 2018 Q3(3) 2024.10.15
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta = 0.5 # 成功確率(固定)
n_values = np.arange(1, 11, 1) # nの値を1から10まで1刻みで変化させる
num_simulations = 100000 # シミュレーション回数
simulated_means = [] # 条件付き期待値のシミュレーション結果
theoretical_means = [] # 条件付き理論期待値
unconditional_means_sim = [] # 条件なしの期待値のシミュレーション結果
unconditional_means_theory = [] # 条件なしの理論期待値
# nを変化させてシミュレーション
for n in n_values:
# 二項分布のサンプリング
binom_samples = np.random.binomial(n, theta, num_simulations)
samples_X_geq_1 = binom_samples[binom_samples >= 1] # X >= 1 の条件に絞る
# シミュレーションによる条件付き期待値
simulated_mean = np.mean(samples_X_geq_1)
simulated_means.append(simulated_mean)
# 条件付き理論期待値
theoretical_mean = n * theta / (1 - (1 - theta) ** n)
theoretical_means.append(theoretical_mean)
# 条件なしの期待値のシミュレーション結果
unconditional_mean_sim = np.mean(binom_samples)
unconditional_means_sim.append(unconditional_mean_sim)
# 条件なしの理論期待値
unconditional_mean_theory = n * theta
unconditional_means_theory.append(unconditional_mean_theory)
# シミュレーション結果と理論値をプロット
plt.plot(n_values, simulated_means, label="条件付きシミュレーション", marker='o', linestyle='--', color='blue')
plt.plot(n_values, theoretical_means, label="条件付き理論値", marker='x', linestyle='-', color='red')
plt.plot(n_values, unconditional_means_sim, label="条件なしシミュレーション", marker='^', linestyle='--', color='purple')
plt.plot(n_values, unconditional_means_theory, label="条件なし理論値", marker='s', linestyle='-', color='green')
# グラフの描画
plt.xlabel("試行回数 n", fontsize=12)
plt.ylabel("期待値 E[X]", fontsize=12)
plt.title("n の変化に対する期待値の比較 (θ = 0.5)", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()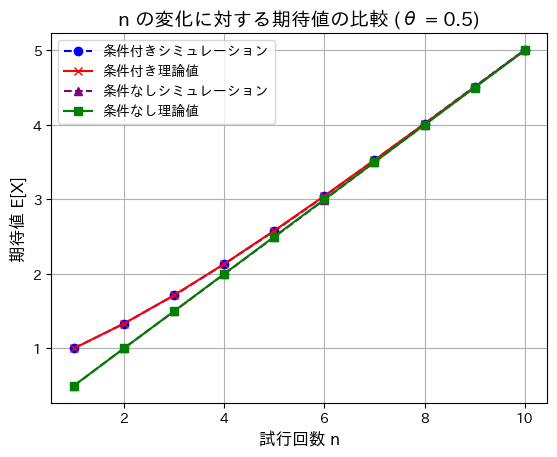
nが増加するほど、条件付きと条件がついていない場合の期待値の差は小さくなります。
分散も同様に確認します。
# 2018 Q3(3) 2024.10.15
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta = 0.5 # 成功確率(固定)
n_values = np.arange(1, 11, 1) # nの値を1から10まで1刻みで変化させる
num_simulations = 100000 # シミュレーション回数
simulated_variances = [] # 条件付き分散のシミュレーション結果
theoretical_variances = [] # 条件付き理論分散
unconditional_variances_sim = [] # 条件なしの分散のシミュレーション結果
unconditional_variances_theory = [] # 条件なしの理論分散
# nを変化させてシミュレーション
for n in n_values:
# 二項分布のサンプリング
binom_samples = np.random.binomial(n, theta, num_simulations)
samples_X_geq_1 = binom_samples[binom_samples >= 1] # X >= 1 の条件に絞る
# シミュレーションによる条件付き分散
simulated_variance = np.var(samples_X_geq_1)
simulated_variances.append(simulated_variance)
# 条件付き理論分散
theoretical_variance = (
(n * theta * (1 - theta)) / (1 - (1 - theta) ** n)
- (n ** 2 * theta ** 2 * (1 - theta) ** n) / (1 - (1 - theta) ** n) ** 2
)
theoretical_variances.append(theoretical_variance)
# 条件なしの分散のシミュレーション結果
unconditional_variance_sim = np.var(binom_samples)
unconditional_variances_sim.append(unconditional_variance_sim)
# 条件なしの理論分散
unconditional_variance_theory = n * theta * (1 - theta)
unconditional_variances_theory.append(unconditional_variance_theory)
# シミュレーション結果と理論値をプロット
plt.plot(n_values, simulated_variances, label="条件付きシミュレーション", marker='o', linestyle='--', color='blue')
plt.plot(n_values, theoretical_variances, label="条件付き理論値", marker='x', linestyle='-', color='red')
plt.plot(n_values, unconditional_variances_sim, label="条件なしシミュレーション", marker='^', linestyle='--', color='purple')
plt.plot(n_values, unconditional_variances_theory, label="条件なし理論値", marker='s', linestyle='-', color='green')
# グラフの描画
plt.xlabel("試行回数 n", fontsize=12)
plt.ylabel("分散 V[X]", fontsize=12)
plt.title("n の変化に対する分散の比較 (θ = 0.5)", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()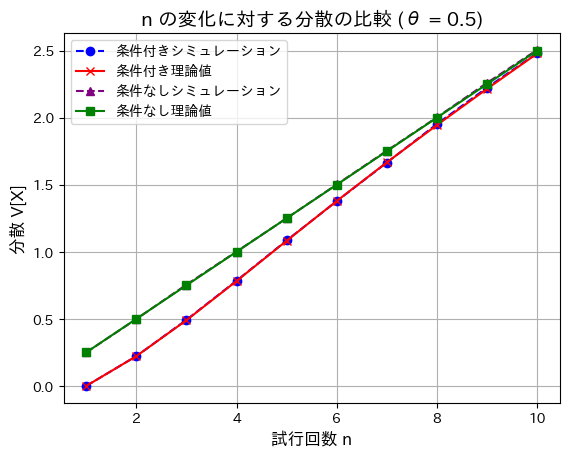
分散も同様に、nが増加するほど差は小さくなりました。