非復元無作為抽出による未知の母数N個の推定を行いました。

コード
複数回シミュレーションし![]() のヒストグラムを描画します。
のヒストグラムを描画します。
# 2018 Q2(5)-1 2024.10.9
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_true = 100 # 真の青球の数 N (これを推定する)
K = 30 # 赤球の数 K (既知)
n = 20 # 抽出する回数
n_trials = 10000 # シミュレーションの試行回数
# 推定量 Nハットのシミュレーション
N_hat_values = []
for _ in range(n_trials):
# 青球 N 個 + 赤球 K 個のボールを作成
balls = [0] * N_true + [1] * K # 0が青球、1が赤球
drawn_balls = np.random.choice(balls, size=n, replace=False) # 非復元抽出
X = np.sum(drawn_balls) # 抽出された赤球の個数
# X を使って N の推定量 N_hat を計算
if X > 0: # Xが0でない場合
N_hat = K * (n - X) / X
N_hat_values.append(N_hat)
# シミュレーション結果の分析
N_hat_mean = np.mean(N_hat_values)
N_hat_var = np.var(N_hat_values)
# 結果表示
print(f"推定量 N_hat の平均: {N_hat_mean}")
print(f"推定量 N_hat の分散: {N_hat_var}")
# ヒストグラム表示
plt.figure(figsize=(10, 6))
plt.hist(N_hat_values, bins=50, density=True, alpha=0.7, color='b', edgecolor='black')
plt.axvline(x=N_true, color='r', linestyle='--', label=f'真の N = {N_true}')
plt.title(f'推定量 N_hat の分布 (N={N_true}, K={K}, n={n})')
plt.xlabel('推定量 N_hat')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()推定量 N_hat の平均: 126.09541441704363
推定量 N_hat の分散: 8070.195087794488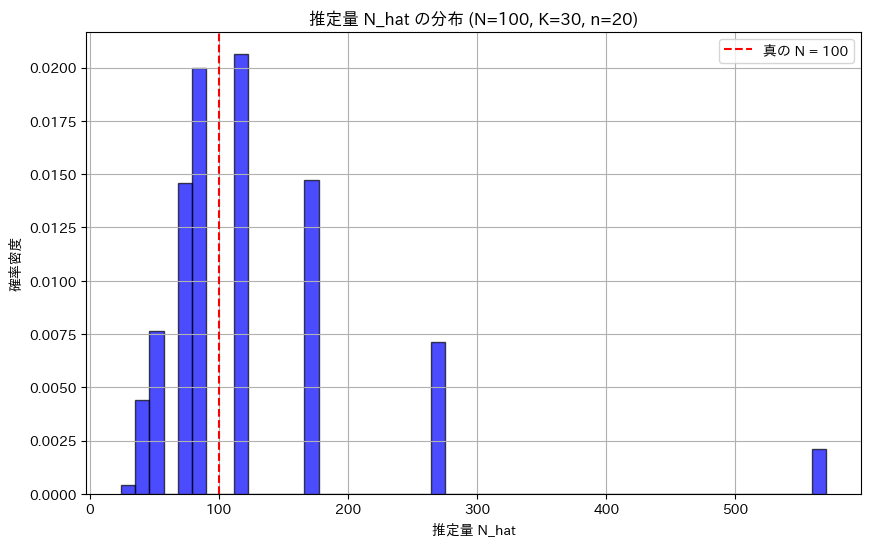
![]() は、真のNから離れた値も取ることがあり、特に飛び飛びの値を取りやすく、右側に裾が長い形をしていることが分かりました。
は、真のNから離れた値も取ることがあり、特に飛び飛びの値を取りやすく、右側に裾が長い形をしていることが分かりました。