非復元無作為抽出の当たり数を確率変数とする確率質量関数を求めました。

コード
超幾何分布HG(N,M,n)に従う確率変数XのシミュレーションをNとMを変化させて実行し理論値と一致するか確認してみます。
# 2018 Q2(3) 2024.10.7
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import hypergeom
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション (列ごとに固定)
M_values = [10, 20, 30, 40, 50] # 赤球の数 M のバリエーション (行ごとに変化)
n = 10 # 抽出する回数
n_trials = 10000 # シミュレーションの試行回数
# グラフのレイアウト設定 (5行x3列)
fig, axes = plt.subplots(5, 3, figsize=(15, 20)) # 5行3列のサブプロット
# 各 M に対してシミュレーションと理論値を計算
for row, M in enumerate(M_values): # 行が M を表す
for col, N in enumerate(N_values): # 列が N を表す
# 理論値の計算
x_values = np.arange(0, n + 1) # 可能な赤球の数 x の範囲
rv = hypergeom(N, M, n) # 超幾何分布のインスタンス
P_X_theory = rv.pmf(x_values) # 理論値(超幾何分布)
# シミュレーションによる確率計算
drawn_red_balls = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M) # 赤球 M 個、青球 N-M 個のリスト
drawn_balls = np.random.choice(balls, size=n, replace=False) # n 回非復元抽出
x = np.sum(drawn_balls) # 赤球の個数を数える
drawn_red_balls.append(x)
# 各サブプロットにグラフを描画
ax = axes[row, col]
ax.plot(x_values, P_X_theory, 'bo-', label=f'理論値 (N={N}, M={M})')
ax.hist(drawn_red_balls, bins=np.arange(-0.5, n + 1.5, 1), density=True, alpha=0.6, color='r', label='シミュレーション結果')
ax.set_xlabel('赤球の個数 (x)')
ax.set_ylabel('確率 P(X = x)')
ax.set_title(f'N={N}, M={M}, n={n}')
ax.grid(True)
# 全体のレイアウト調整
plt.tight_layout()
plt.show()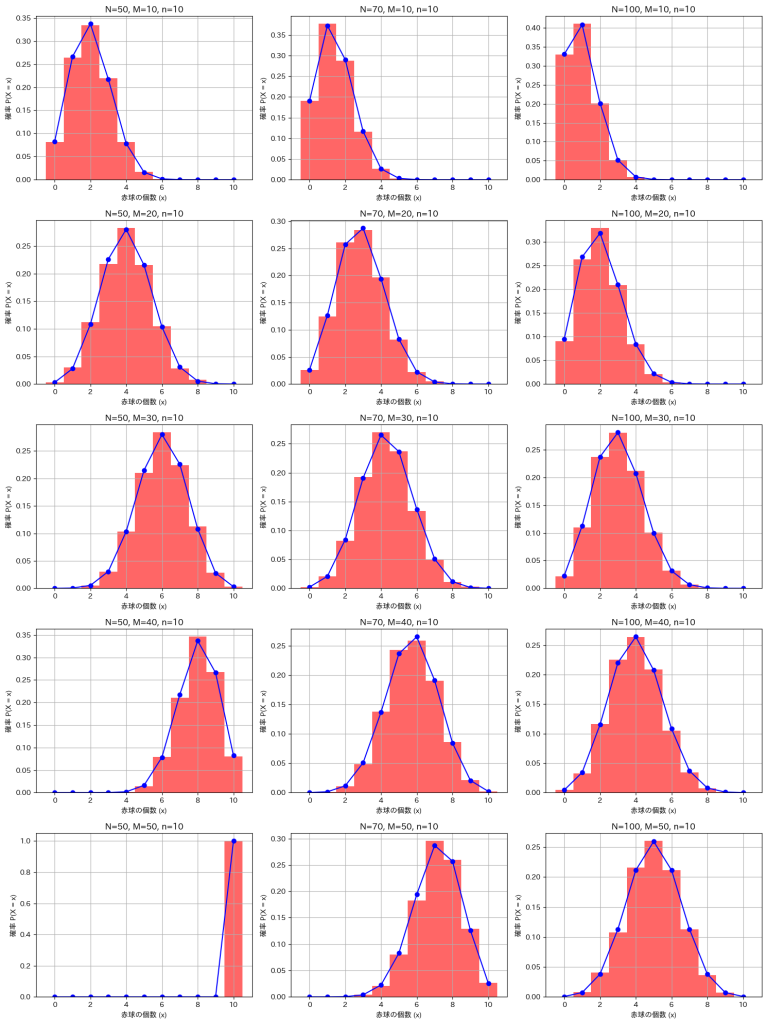
シミュレーションによる結果は理論値と一致しました。