非復元無作為抽出の期待値と分散と共分散を求めました。
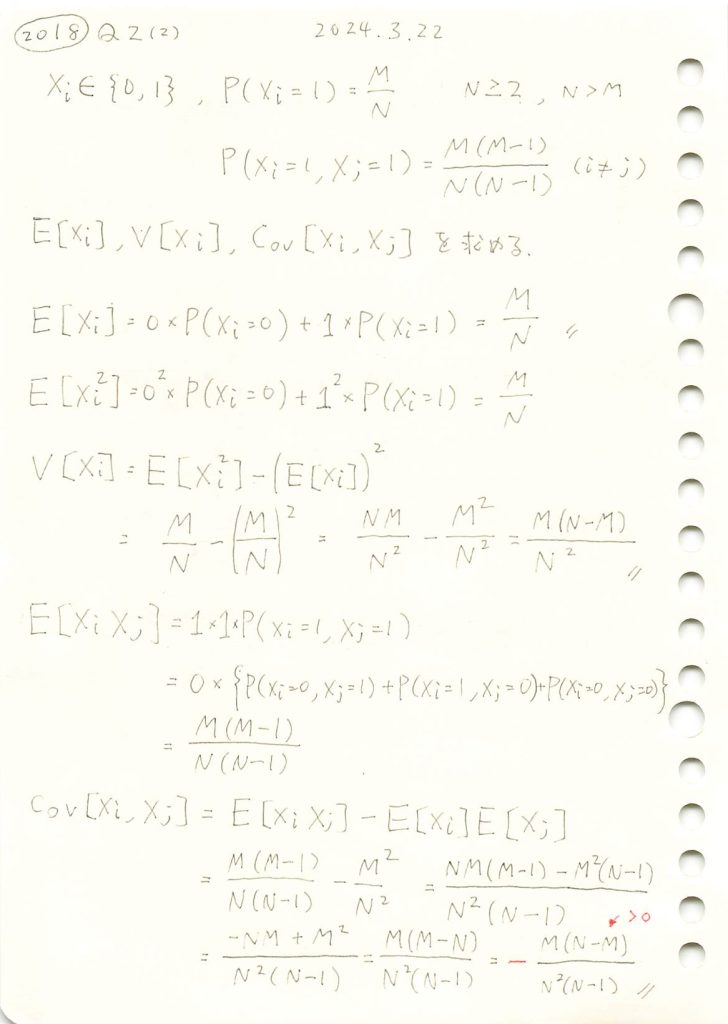
コード
NとMを変化させて期待値E[Xi]についてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(2) 2024.10.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n_trials = 10000 # シミュレーションの試行回数
# 期待値 E[X_i] のグラフ描画
plt.figure(figsize=(10, 6))
for N in N_values:
M_values = np.arange(2, N + 1, M_steps) # 赤球数をステップで変化
# 理論値の計算
E_Xi_theory = M_values / N
# シミュレーションによる期待値の計算
E_Xi_simulation = []
for M in M_values:
count_Xi_1 = 0
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_ball = np.random.choice(balls, size=1, replace=False)
count_Xi_1 += drawn_ball[0]
E_Xi_simulation.append(count_Xi_1 / n_trials)
# グラフに追加描画
plt.plot(M_values, E_Xi_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, E_Xi_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
plt.xlabel('赤球の数 (M)')
plt.ylabel('期待値 E[X_i]')
plt.title('異なる N における 期待値 E[X_i] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()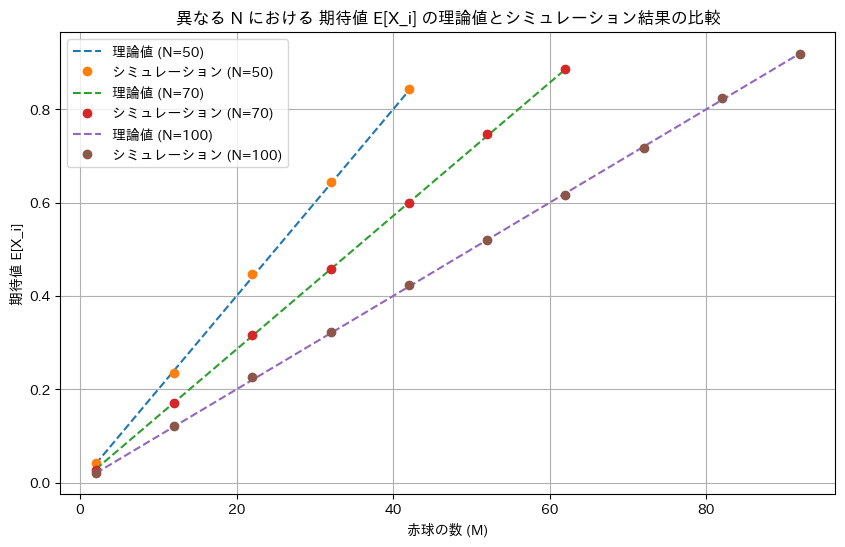
ミュレーションによる結果は理論値と一致しました。
次に、分散V[Xi]についてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(2) 2024.10.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n_trials = 10000 # シミュレーションの試行回数
# 分散 V[X_i] のグラフ描画
plt.figure(figsize=(10, 6))
for N in N_values:
M_values = np.arange(2, N + 1, M_steps)
# 理論値の計算
V_Xi_theory = M_values * (N - M_values) / N**2
# シミュレーションによる分散の計算
V_Xi_simulation = []
for M in M_values:
Xi_values = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_ball = np.random.choice(balls, size=1, replace=False)
Xi_values.append(drawn_ball[0])
V_Xi_simulation.append(np.var(Xi_values))
# グラフに追加描画
plt.plot(M_values, V_Xi_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, V_Xi_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
plt.xlabel('赤球の数 (M)')
plt.ylabel('分散 V[X_i]')
plt.title('異なる N における 分散 V[X_i] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()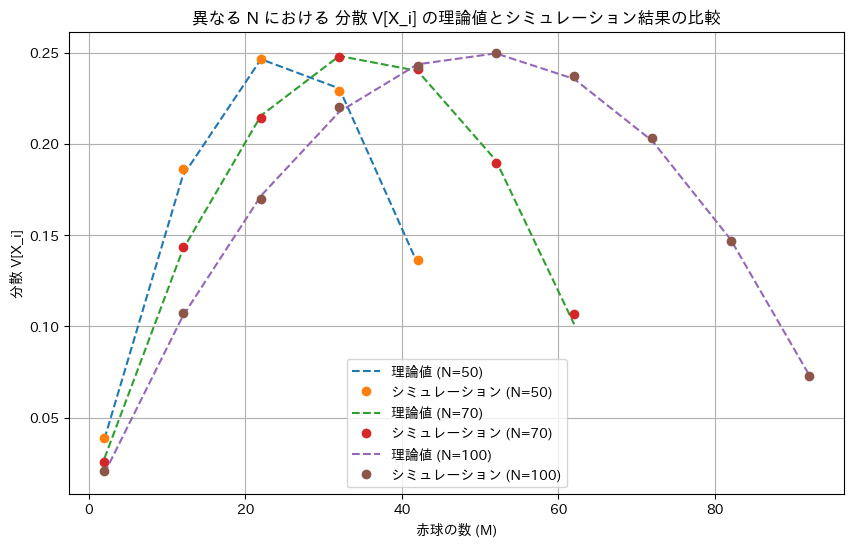
ミュレーションによる結果は理論値と一致しました。
次に、共分散Cov[Xi,Xj]についてシミュレーションを行い理論値と一致するか確認します。ただし、共分散は二変数を扱うため誤差が大きくなりやすいので、シミュレーションの試行回数を多め(1,000,000回)でやってみます。実行は環境により数十分かかることもあります。
# 2018 Q2(2) 2024.10.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n_trials = 1000000 # シミュレーションの試行回数
# 共分散 Cov[X_i, X_j] のグラフ描画
plt.figure(figsize=(10, 6))
for N in N_values:
M_values = np.arange(2, N + 1, M_steps)
# 理論値の計算
Cov_Xi_Xj_theory = -(M_values * (N - M_values)) / (N**2 * (N - 1))
# シミュレーションによる共分散の計算
Cov_Xi_Xj_simulation = []
for M in M_values:
Xi_values = []
Xj_values = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_balls = np.random.choice(balls, size=2, replace=False)
Xi_values.append(drawn_balls[0])
Xj_values.append(drawn_balls[1])
Cov_Xi_Xj_simulation.append(np.cov(Xi_values, Xj_values)[0, 1])
# グラフに追加描画
plt.plot(M_values, Cov_Xi_Xj_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, Cov_Xi_Xj_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
plt.xlabel('赤球の数 (M)')
plt.ylabel('共分散 Cov[X_i, X_j]')
plt.title('異なる N における 共分散 Cov[X_i, X_j] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()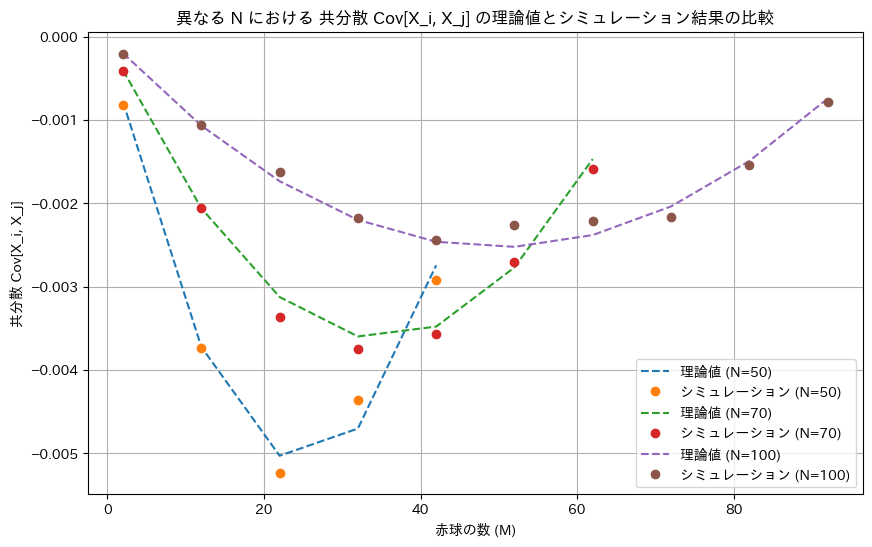
シミュレーションによる結果は概ね一致しました。