不偏分散の平方根の期待値に於いて、母標準偏差に対する偏りを求めました。
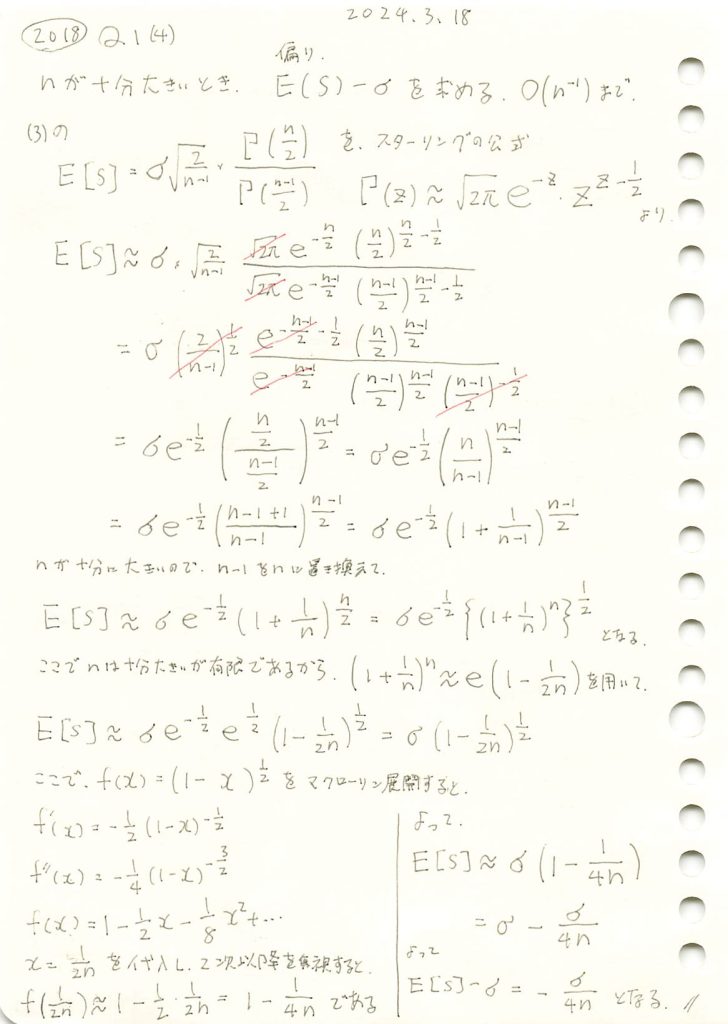
コード
数値シミュレーションでE[S] 求め、理論値![]() と一致するか確認します。
と一致するか確認します。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 2 # 母標準偏差
n_values = np.array([10, 20, 50, 100, 200]) # サンプルサイズの値
num_simulations = 10000 # シミュレーションの回数
# 結果を格納するリスト
simulated_means = []
theoretical_means = []
sigma_values = [sigma] * len(n_values) # 母標準偏差の値をリストで作成
# シミュレーション実行
for n in n_values:
# カイ二乗分布に従う乱数を生成
chi_squared_samples = np.random.chisquare(df=n-1, size=num_simulations)
# 標本標準偏差 S のシミュレーション
S_simulation = sigma * np.sqrt(chi_squared_samples / (n - 1))
# シミュレーションの期待値 (平均)
simulated_mean = np.mean(S_simulation)
simulated_means.append(simulated_mean)
# 理論値 E[S] = σ - σ / (4n)
theoretical_mean = sigma - sigma / (4 * n)
theoretical_means.append(theoretical_mean)
# 結果表示
for i, n in enumerate(n_values):
print(f"n = {n}: シミュレーション平均 = {simulated_means[i]:.4f}, 理論値 = {theoretical_means[i]:.4f}, 母標準偏差 = {sigma:.4f}")
# グラフ描画
plt.figure(figsize=(8, 6))
plt.plot(n_values, simulated_means, 'bo-', label='シミュレーション平均')
plt.plot(n_values, theoretical_means, 'r--', label='理論値')
plt.plot(n_values, sigma_values, 'g-', label='母標準偏差 σ')
plt.xlabel('サンプルサイズ n')
plt.ylabel('期待値 E[S]')
plt.title('標本標準偏差 E[S] のシミュレーションと理論値の比較')
plt.legend()
plt.grid(True)
plt.show()n = 10: シミュレーション平均 = 1.9394, 理論値 = 1.9500, 母標準偏差 = 2.0000
n = 20: シミュレーション平均 = 1.9747, 理論値 = 1.9750, 母標準偏差 = 2.0000
n = 50: シミュレーション平均 = 1.9888, 理論値 = 1.9900, 母標準偏差 = 2.0000
n = 100: シミュレーション平均 = 1.9961, 理論値 = 1.9950, 母標準偏差 = 2.0000
n = 200: シミュレーション平均 = 1.9974, 理論値 = 1.9975, 母標準偏差 = 2.0000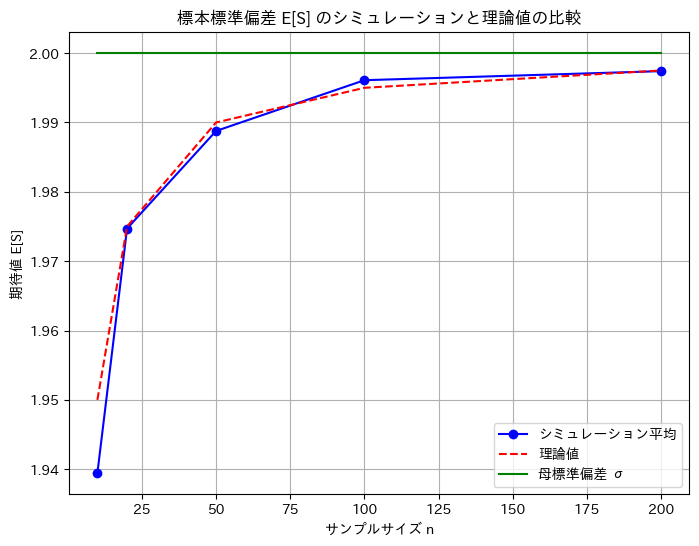
数値シミュレーションでのE[S]は、理論値![]() に一致することが確認できました。
に一致することが確認できました。