重回帰モデルの重みの推定量の分散を求め、説明変数間の相関がそれにどのように影響するか確認しました。
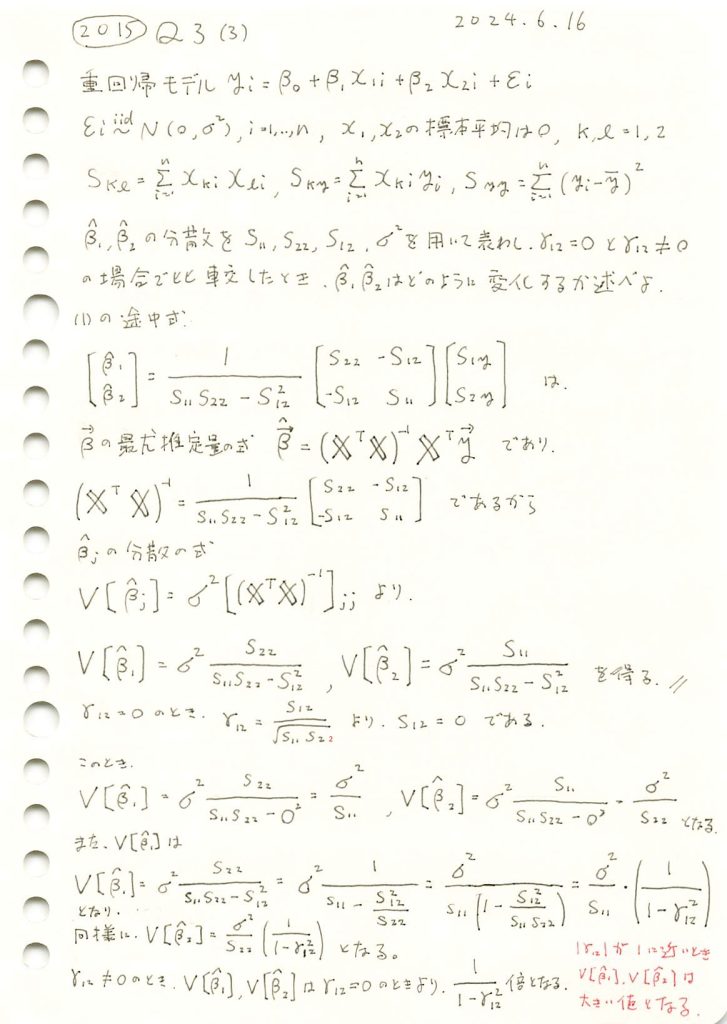
コード
の変化が
と
に与える影響を、グラフで描画して確認します。
# 2015 Q3(3) 2024.12.14
import numpy as np
import matplotlib.pyplot as plt
# 1. パラメータ設定
r12_vals = np.linspace(-0.99, 0.99, 200) # r12の値（-0.99から0.99まで）
sigma2 = 1 # 分散 σ^2
S11 = 10 # S11の仮定値
S22 = 15 # S22の仮定値
# 2. 分散の計算
Var_beta1 = (sigma2 / S11) * (1 / (1 - r12_vals**2)) # Var(β1)
Var_beta2 = (sigma2 / S22) * (1 / (1 - r12_vals**2)) # Var(β2)
# 3. グラフのプロット
plt.figure(figsize=(10, 6))
plt.plot(r12_vals, Var_beta1, label=r'$\mathrm{Var}(\hat{\beta}_1)$', color='blue', linewidth=2)
plt.plot(r12_vals, Var_beta2, label=r'$\mathrm{Var}(\hat{\beta}_2)$', color='orange', linewidth=2)
plt.axhline(y=sigma2 / S11, color='blue', linestyle='--', label=r'$r_{12}=0$ の $\mathrm{Var}(\hat{\beta}_1)$')
plt.axhline(y=sigma2 / S22, color='orange', linestyle='--', label=r'$r_{12}=0$ の $\mathrm{Var}(\hat{\beta}_2)$')
# 軸ラベルとタイトル
plt.title(r'$\mathrm{Var}(\hat{\beta}_1)$ と $\mathrm{Var}(\hat{\beta}_2)$ の $r_{12}$ に対する変化', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}$（$x_1$と$x_2$の相関）', fontsize=12)
plt.ylabel(r'分散', fontsize=12)
# 凡例とグリッド
plt.legend(fontsize=10, loc='upper right')
plt.grid(alpha=0.5)
# グラフ表示
plt.tight_layout()
plt.show()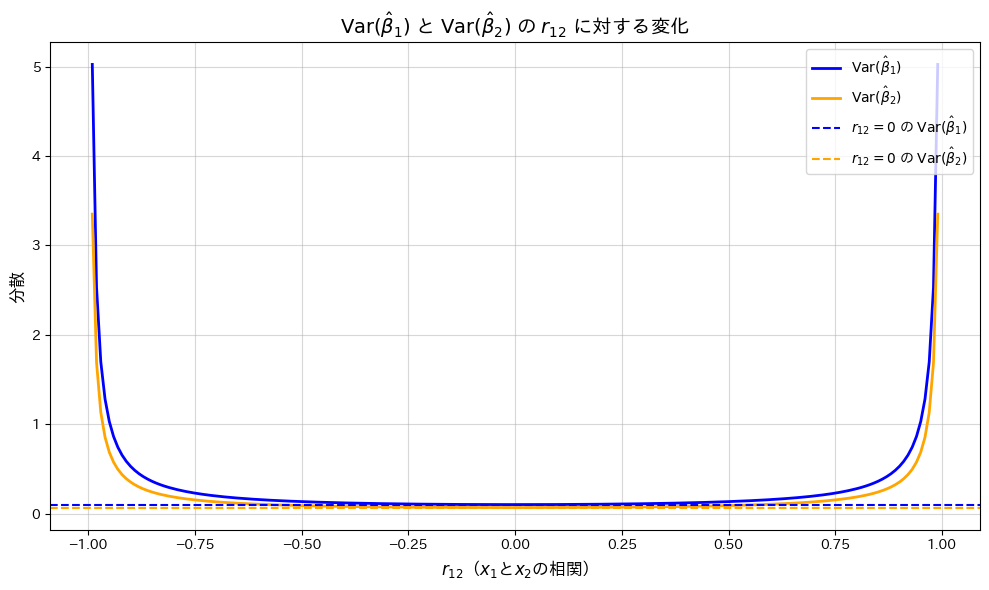
が0に近いほどとは最小となり、相関が高まると分散が増加することが確認されました。