重回帰モデルの重みβ1を３つの相関係数を使って表し、それが負になる必要十分条件を求めました。
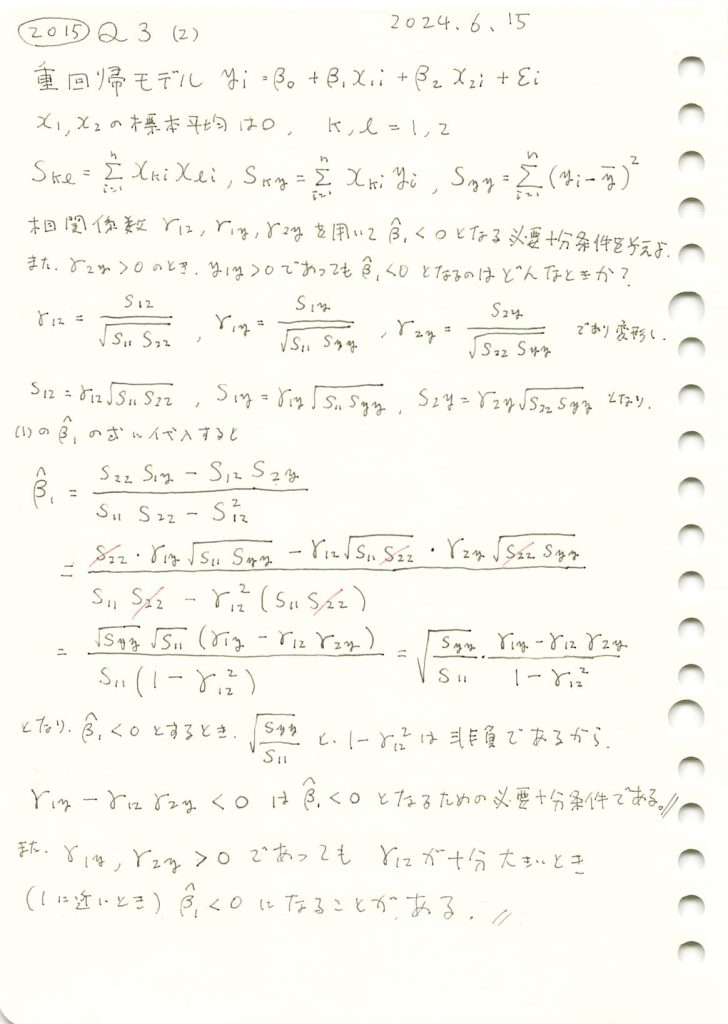
コード
が大きな値をとる場合、
が負の値をとりやすくなることを確認するため、とは、正の数に固定した上で、グラフで可視化します。
# 2015 Q3(2) 2024.12.13
import numpy as np
import matplotlib.pyplot as plt
# 1. パラメータの設定
n = 100 # サンプルサイズ
r12_vals = np.linspace(-0.99, 0.99, 100) # r12 を -0.99 から 0.99 まで変化させる
r1y = 0.5 # r1y を固定
r2y = 0.6 # r2y を固定
# 2. Beta1 の計算
beta1_vals = []
for r12 in r12_vals:
if abs(r12) >= 1:
beta1_vals.append(np.nan) # r12 = ±1 の場合は計算不能
continue
beta1 = (r1y - r12 * r2y) / (1 - r12**2) # 簡略化された Beta1 の符号条件
beta1_vals.append(beta1)
# 3. 結果の可視化
plt.figure(figsize=(8, 6))
plt.plot(r12_vals, beta1_vals, label=r'$\hat{\beta}_1$', color='blue')
plt.axhline(0, color='red', linestyle='--', label='ゼロライン (基準)')
plt.title(r'$\hat{\beta}_1$ と $r_{12}$ の関係', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}$（$x_1$と$x_2$の相関）', fontsize=12)
plt.ylabel(r'$\hat{\beta}_1$', fontsize=12)
plt.legend(fontsize=10, loc='upper left')
plt.grid(alpha=0.7)
plt.tight_layout()
plt.show()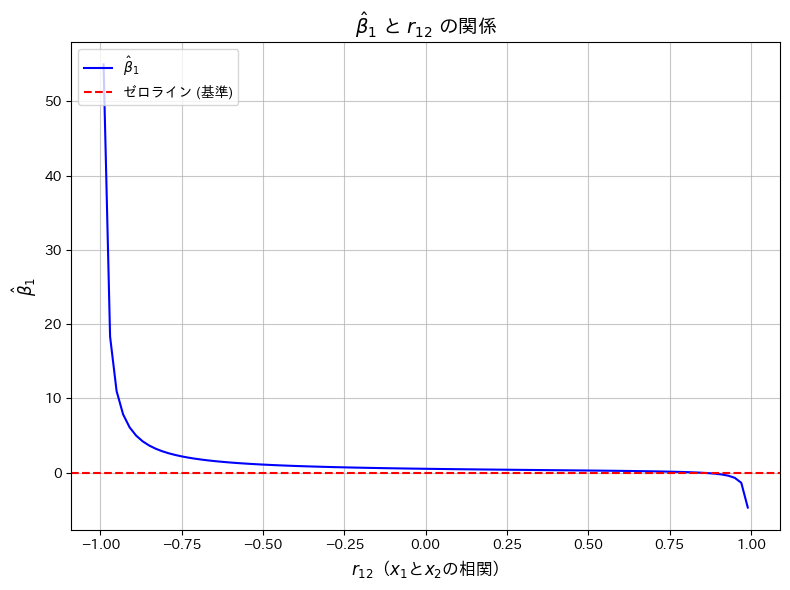
が1に近い値をとると、が負の値をとる傾向があることが確認できました。