線形関係のある確率変数との相関係数や条件付き確率分布を求めました。

コード
(1) Zが![]() に従うかシミュレーションし確かめます。
に従うかシミュレーションし確かめます。
# 2017 Q4(1) 2024.11.6
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定数の設定
a = 1
k = 2
num_samples = 10000
# シミュレーション
X = np.random.normal(0, 1, num_samples)
Y = np.random.normal(0, 1, num_samples)
Z = a + k * X + Y
# 理論値の計算
mean_theory = a
std_dev_theory = np.sqrt(k**2 + 1)
# シミュレーションによる値の計算
mean_simulation = np.mean(Z)
std_dev_simulation = np.std(Z)
# 理論値とシミュレーションによる値の表示
print(f"理論上の期待値: {mean_theory}")
print(f"シミュレーションによる期待値: {mean_simulation}")
print(f"理論上の標準偏差: {std_dev_theory}")
print(f"シミュレーションによる標準偏差: {std_dev_simulation}")
# ヒストグラムのプロット
plt.hist(Z, bins=50, density=True, alpha=0.6, color='b', label="シミュレーションによる Z の分布")
# 理論分布のプロット
x_vals = np.linspace(min(Z), max(Z), 100)
plt.plot(x_vals, norm.pdf(x_vals, mean_theory, std_dev_theory), 'r', label="理論分布 N(a, k^2 + 1)")
# グラフのラベル
plt.title("Z の分布")
plt.xlabel("Z の値")
plt.ylabel("密度")
plt.legend()
plt.show()理論上の期待値: 1
シミュレーションによる期待値: 0.9814460670948696
理論上の標準偏差: 2.23606797749979
シミュレーションによる標準偏差: 2.2474915102454482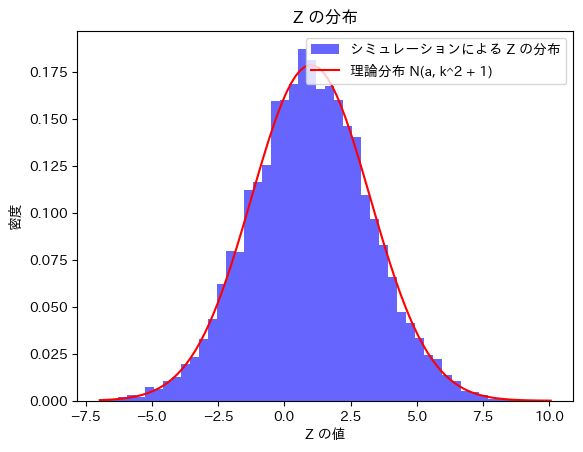
Zは![]() に従うことが確認できました。
に従うことが確認できました。
(2) 次に、XとZの相関係数をシミュレーションにより求めます。
# 2017 Q4(2) 2024.11.6
import numpy as np
import matplotlib.pyplot as plt
# 定数の設定
a = 1
k = 2
num_samples = 10000
# シミュレーション
X = np.random.normal(0, 1, num_samples)
Y = np.random.normal(0, 1, num_samples)
Z = a + k * X + Y
# 理論的な相関係数の計算
correlation_theory = k / np.sqrt(k**2 + 1)
# シミュレーションによる相関係数の計算
correlation_simulated = np.corrcoef(X, Z)[0, 1]
# 理論値とシミュレーションによる相関係数の表示
print(f"理論上の相関係数: {correlation_theory}")
print(f"シミュレーションによる相関係数: {correlation_simulated}")
# 相関係数の視覚化のための散布図のプロット
plt.figure(figsize=(8, 6))
plt.scatter(X, Z, alpha=0.5, s=10, label="X と Z の散布図")
plt.title("X と Z の相関関係")
plt.xlabel("X の値")
plt.ylabel("Z の値")
plt.legend()
plt.show()理論上の相関係数: 0.8944271909999159
シミュレーションによる相関係数: 0.8943931884333798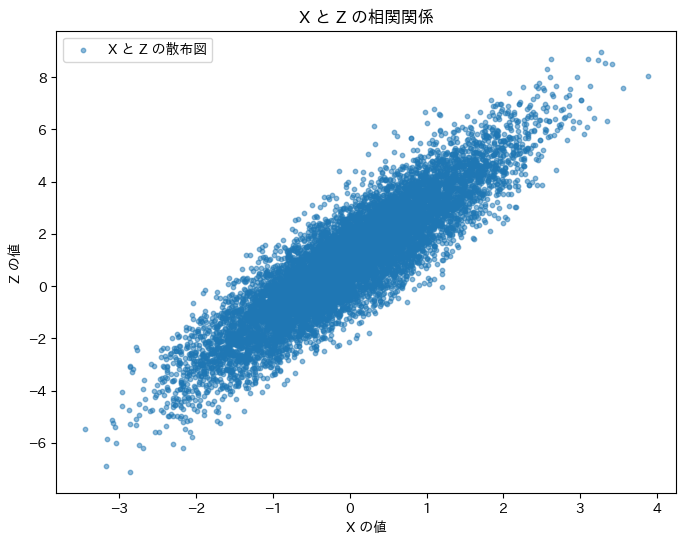
XとZの相関係数は理論値と一致しました。
(3) 次に、Z|X=xがN(a+kx,1)に従うかシミュレーションし確かめます。
# 2017 Q4(3) 2024.11.6
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定数の設定
a = 1
k = 2
num_samples = 10000
x_fixed = 0.5 # 条件として与える X の値
# シミュレーション
Z_given_X = a + k * x_fixed + np.random.normal(0, 1, num_samples)
# 理論値の計算
mean_conditional = a + k * x_fixed
std_dev_conditional = 1 # 分散が 1 であるため
# シミュレーションによる値の計算
mean_simulation = np.mean(Z_given_X)
std_dev_simulation = np.std(Z_given_X)
# 理論値とシミュレーションによる値の表示
print(f"理論上の期待値 (Z | X = {x_fixed}): {mean_conditional}")
print(f"シミュレーションによる期待値: {mean_simulation}")
print(f"理論上の標準偏差: {std_dev_conditional}")
print(f"シミュレーションによる標準偏差: {std_dev_simulation}")
# 条件付き分布のヒストグラムのプロット
plt.hist(Z_given_X, bins=50, density=True, alpha=0.6, color='g', label=f"シミュレーションによる Z | X = {x_fixed} の分布")
# 理論分布のプロット
z_vals = np.linspace(min(Z_given_X), max(Z_given_X), 100)
plt.plot(z_vals, norm.pdf(z_vals, mean_conditional, std_dev_conditional), 'r', label="理論分布 N(a + kx, 1)")
# グラフの装飾
plt.title(f"条件付き分布 Z | X = {x_fixed}")
plt.xlabel("Z の値")
plt.ylabel("密度")
plt.legend()
plt.show()理論上の期待値 (Z | X = 0.5): 2.0
シミュレーションによる期待値: 1.978029240745398
理論上の標準偏差: 1
シミュレーションによる標準偏差: 1.0089203051741882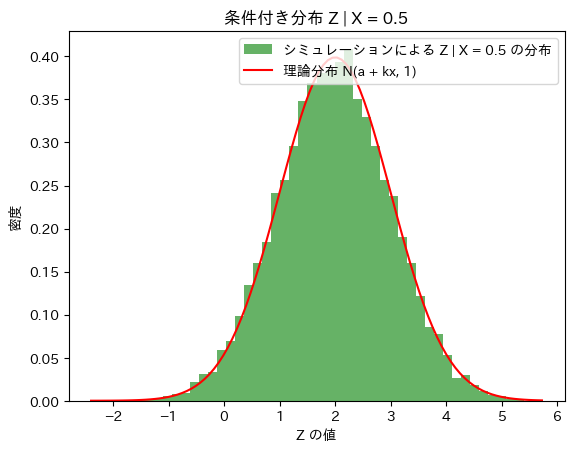
Z|X=xはN(a+kx,1)に従うことが確認できました。