標準化されたポアソン分布はパラメータλを∞に近づけると標準正規分布に収束することを示しました。
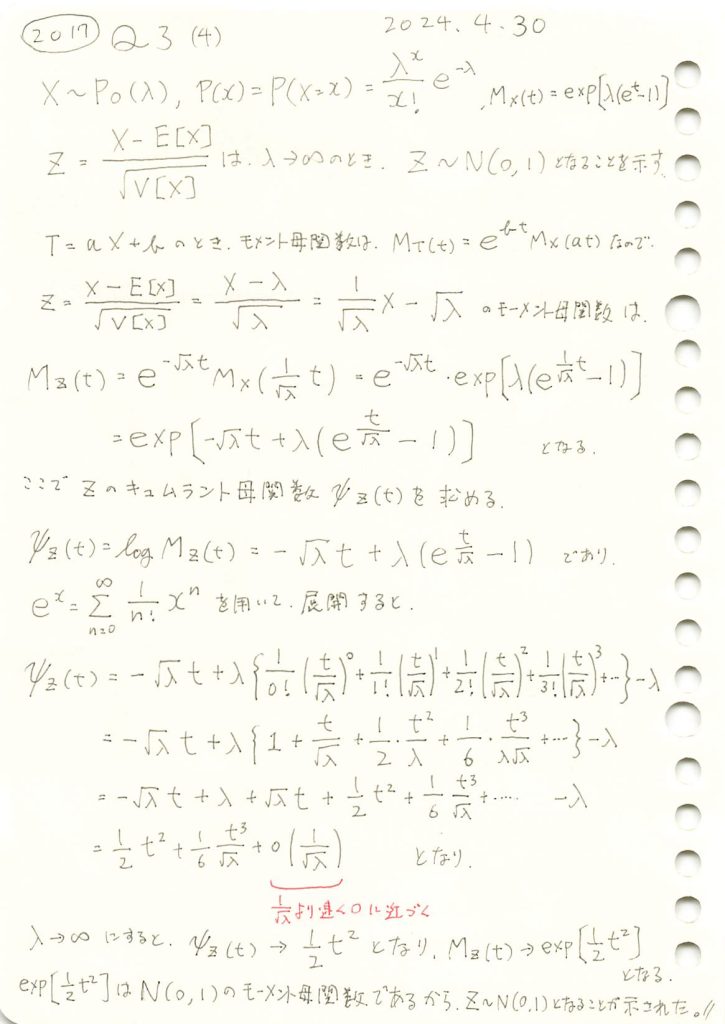
コード
λを変化させて標準化されたポアソン分布Zの分布をシミュレーションにより確認してみます。
# 2017 Q3(4) 2024.11.05
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# パラメータ設定
lambda_values = [10, 20, 50, 100]
sample_size = 10000 # サンプルサイズ
# 標準正規分布の理論値
z_values = np.linspace(-4, 4, 100)
normal_pdf = norm.pdf(z_values, 0, 1)
# 2x2 のグリッドでプロット
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel()
# 各 λ に対してヒストグラムをプロット
for i, lambda_val in enumerate(lambda_values):
# ポアソン分布からサンプルを生成し、標準化
X_samples = np.random.poisson(lambda_val, sample_size)
Z_samples = (X_samples - lambda_val) / np.sqrt(lambda_val)
# 各 λ に対応するサブプロットでヒストグラムを描画
axes[i].hist(Z_samples, bins=100, density=True, alpha=0.5, color='orange', label=f"λ = {lambda_val}")
axes[i].plot(z_values, normal_pdf, color="red", linestyle="--", label="標準正規分布 N(0, 1)")
# グラフのカスタマイズ
axes[i].set_ylim(0, 1.8)
axes[i].set_xlabel("標準化変量 Z")
axes[i].set_ylabel("確率密度")
axes[i].set_title(f"標準化されたポアソン分布 (λ = {lambda_val})")
axes[i].legend()
axes[i].grid(True)
# レイアウト調整
plt.tight_layout()
plt.show()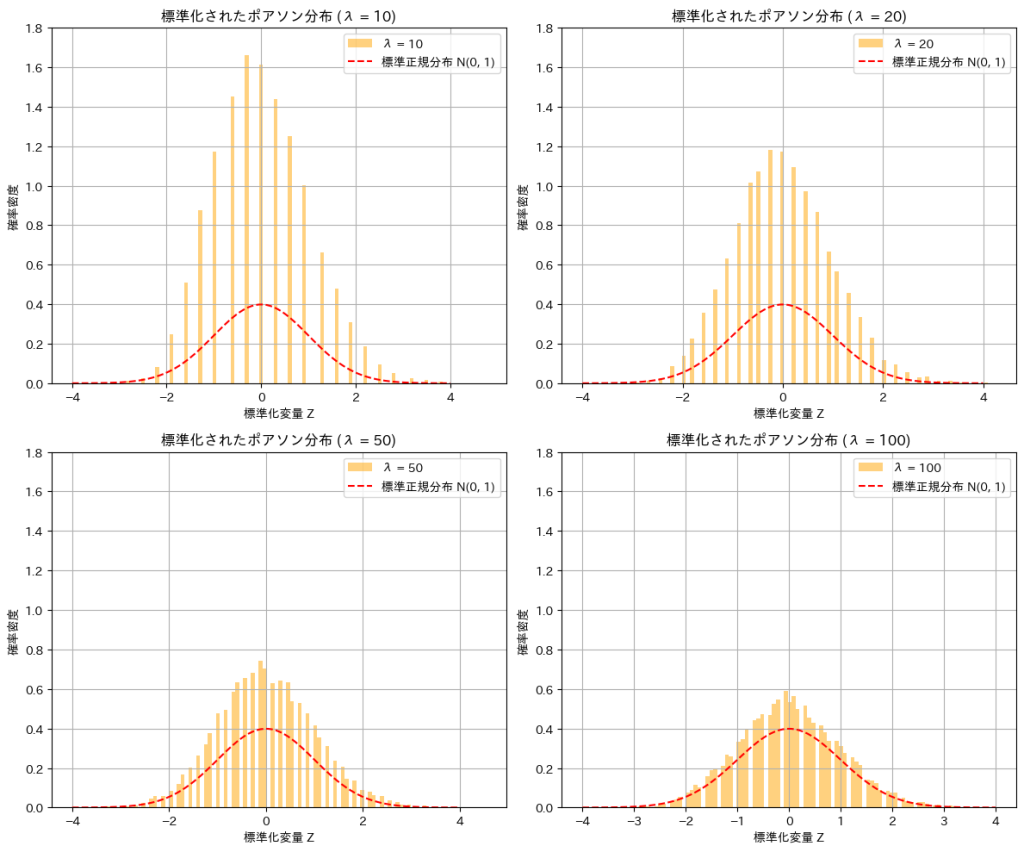
λ が増加するにつれて、標準化されたポアソン分布 Z の分布が標準正規分布に近づくことが確認できました。