ポアソン分布のモーメント母関数を求めて、それを使って期待値と分散を求めました。

コード
ポアソン分布のパラメータλを変化させシミュレーションし期待と分散が共にλになるか確認しました。
# 2017 Q3(2) 2024.11.3
import numpy as np
import matplotlib.pyplot as plt
# λの範囲を定義
lambda_values = np.arange(1, 21)
sample_size = 10000 # 各λに対するサンプル数
# サンプル平均と分散を格納するリスト
sample_means = []
sample_variances = []
# 各λに対するシミュレーションを実行
for lambda_val in lambda_values:
# ポアソン分布のサンプルを生成
samples = np.random.poisson(lambda_val, sample_size)
# サンプルの平均と分散を計算
sample_means.append(np.mean(samples))
sample_variances.append(np.var(samples))
# 結果をプロット
plt.figure(figsize=(12, 6))
# サンプル平均と理論値をプロット
plt.plot(lambda_values, sample_means, label="サンプル平均 (期待値)", marker='o')
plt.plot(lambda_values, lambda_values, label="理論値 (期待値)", linestyle='--')
# サンプル分散と理論値をプロット
plt.plot(lambda_values, sample_variances, label="サンプル分散", marker='x')
plt.plot(lambda_values, lambda_values, label="理論値 (分散)", linestyle=':')
# グラフのカスタマイズ
plt.xlabel("λ")
plt.ylabel("期待値 / 分散")
plt.title("ポアソン分布の期待値と分散の可視化 (λの関数として)")
plt.legend()
plt.grid(True)
plt.show()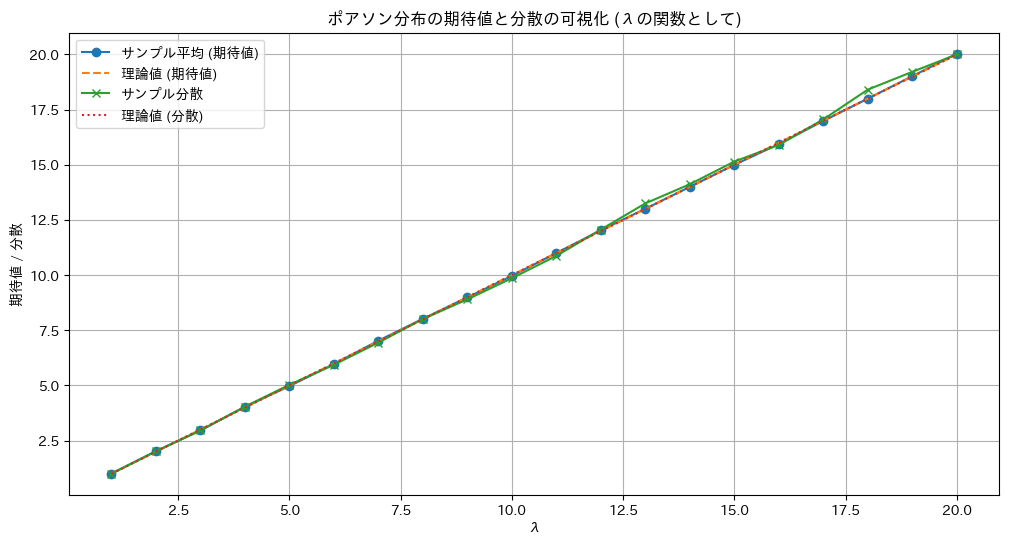
ポアソン分布の期待と分散が共にλになることが確認できました。