重回帰モデルにおいて正規方程式を用い、各重みの最小二乗推定量を求めました。
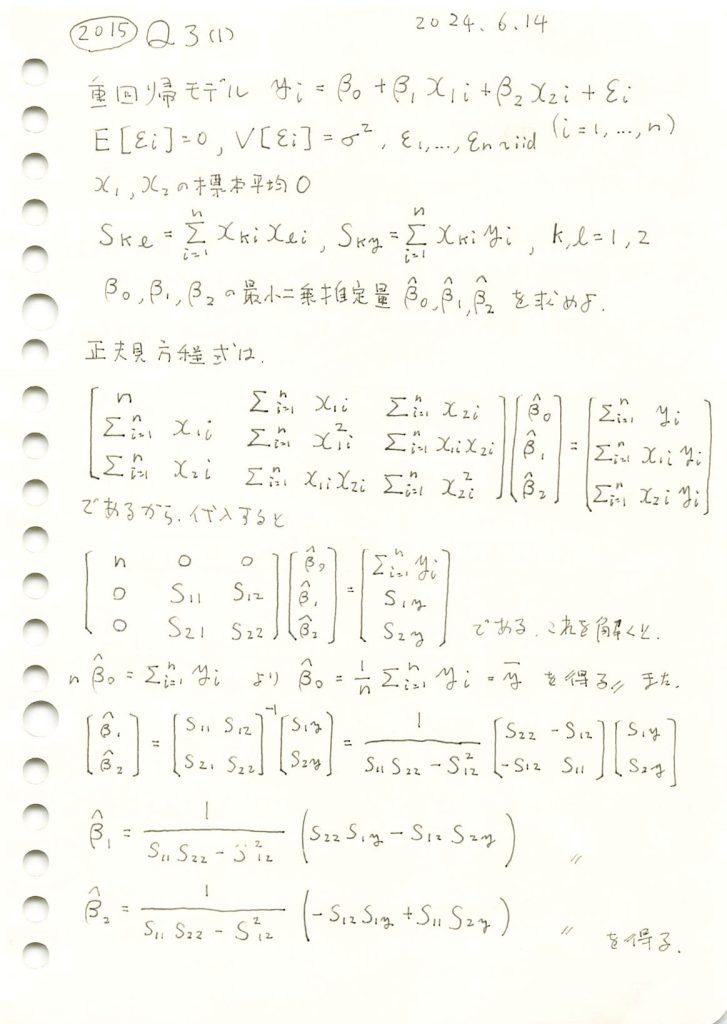
コード
重回帰モデルのシミュレーションを行い、パラメータβ0,β1,β2の推定量を計算し、真の値と比較します。
# 2015 Q3(1) 2024.12.12
import numpy as np
# 1. パラメータの設定 (再現性のため同じ設定を使用)
n = 100
beta_0, beta_1, beta_2 = 2.0, 1.0, -0.5
sigma = 1.0
# 2. 説明変数と誤差の生成
x1 = np.random.randn(n)
x2 = np.random.randn(n)
epsilon = np.random.randn(n) * sigma
# 3. 応答変数の生成
y = beta_0 + beta_1 * x1 + beta_2 * x2 + epsilon
# 4. S11, S22, S12, S1y, S2y を計算
S11 = np.sum(x1**2)
S22 = np.sum(x2**2)
S12 = np.sum(x1 * x2)
S1y = np.sum(x1 * y)
S2y = np.sum(x2 * y)
# 5. 推定値の計算 (導出した式に基づく)
denominator = S11 * S22 - S12**2
beta1_hat = (S22 * S1y - S12 * S2y) / denominator
beta2_hat = (S11 * S2y - S12 * S1y) / denominator
beta0_hat = np.mean(y) - beta1_hat * np.mean(x1) - beta2_hat * np.mean(x2)
# 推定値の表示
print(f"推定値 (導出した式):")
print(f" β0 = {beta0_hat:.3f}")
print(f" β1 = {beta1_hat:.3f}")
print(f" β2 = {beta2_hat:.3f}")
# 真の値と比較
print("\n真の値:")
print(f" β0 = {beta_0:.3f}")
print(f" β1 = {beta_1:.3f}")
print(f" β2 = {beta_2:.3f}")推定値 (導出した式):
β0 = 1.909
β1 = 0.863
β2 = -0.505
真の値:
β0 = 2.000
β1 = 1.000
β2 = -0.500シミュレーションの結果、パラメータβ0,β1,β2の推定量はわずかな誤差はあるものの、真の値に近い値を示しました。