正規分布の分散の最尤推定量を母平均が既知の場合と未知の場合でそれぞれ求めましまた。

コード
サンプルサイズnを50に固定し尤度関数を可視化します。また最尤推定量 ![]() と
と![]() をプロットしてみます。
をプロットしてみます。
# 2017 Q1(5) 2024.10.28
# 最尤推定量 (T^2, S^2) の計算と尤度関数の可視化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# シミュレーションパラメータの設定
mu = 5.0 # 母平均(既知)
sigma = 2.0 # 母標準偏差(√母分散)
selected_sample_size = 50 # 固定サンプルサイズ
true_variance = sigma**2 # 母分散
# 正規分布からのサンプル生成(サンプルサイズは selected_sample_size で固定)
sample = np.random.normal(mu, sigma, selected_sample_size) # 固定サンプル生成
# 最尤推定量の計算
T2 = np.sum((sample - mu) ** 2) / selected_sample_size # 最尤推定量 T^2 の計算 (μが既知)
sample_mean = np.mean(sample)
S2 = np.sum((sample - sample_mean) ** 2) / (selected_sample_size - 1) # 最尤推定量 S^2 の計算 (μが未知)
# 尤度関数のプロットのためのパラメータ設定
sigma_squared_trial_values = np.linspace(0.1, 5.0, 100) # σ^2 の値を試行的に設定
likelihoods = [] # 尤度関数の値を保存するリスト
# 尤度関数の計算(固定サンプルに基づく)
for sigma_squared_trial in sigma_squared_trial_values:
likelihood = np.prod(norm.pdf(sample, loc=mu, scale=np.sqrt(sigma_squared_trial))) # 尤度関数の値を計算
likelihoods.append(likelihood)
# グラフの作成
plt.figure(figsize=(10, 6))
plt.plot(sigma_squared_trial_values, likelihoods, label='尤度関数', color='blue')
plt.axvline(x=T2, color='green', linestyle='--', label='$T^2$ (最尤推定量, μが既知)', linewidth=2)
plt.axvline(x=S2, color='orange', linestyle='--', label='$S^2$ (最尤推定量, μが未知)', linewidth=2)
plt.axvline(x=true_variance, color='red', linestyle='-.', label='母分散 $\\sigma^2$', linewidth=2)
plt.title(f'サンプルサイズ {selected_sample_size} における尤度関数と推定量の比較')
plt.xlabel('$\sigma^2$ の試行値')
plt.ylabel('尤度')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()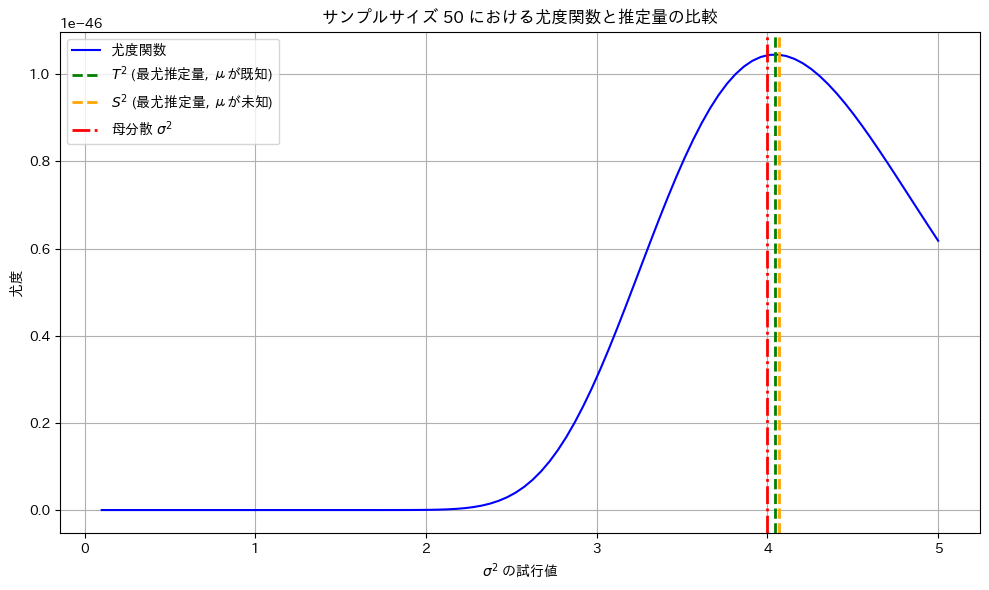
最尤推定量 ![]() と
と![]() は尤度が最大となる
は尤度が最大となる![]() の値を取っています。
の値を取っています。
もう一度実行してみます。
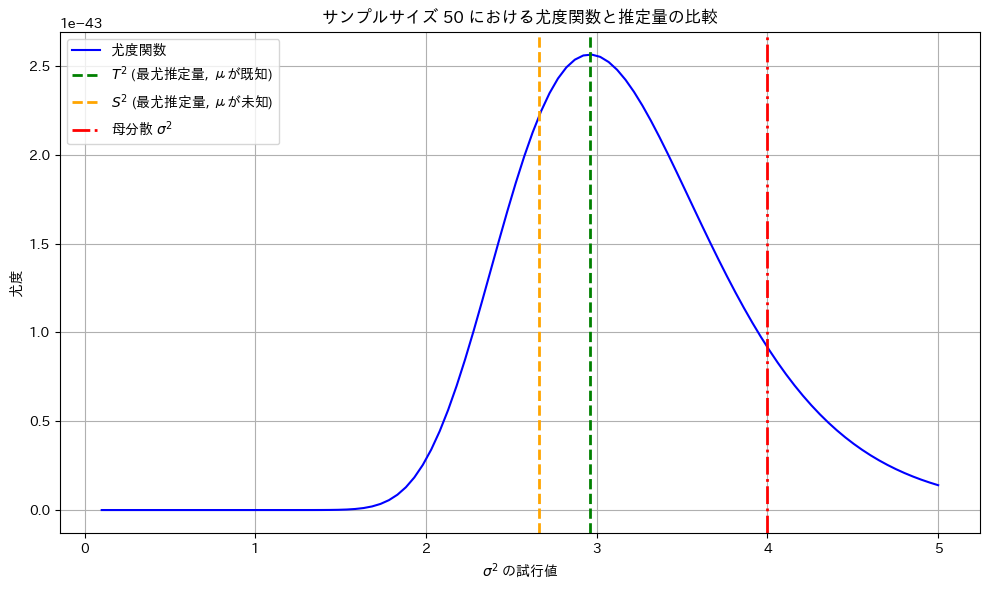
サンプルによっては最尤推定量![]() と
と![]() は
は![]() から乖離する場合もあります。
から乖離する場合もあります。
次に、サンプルサイズを大きくすることで母分散に近づくことを確認します。
# 2017 Q1(5) 2024.10.28
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
mu = 5.0 # 母平均(既知)
sigma = 2.0 # 母標準偏差(√母分散)
true_variance = sigma**2 # 母分散
sample_sizes = range(50, 10050, 50) # サンプルサイズを設定
# シミュレーション結果を保存するリスト
T2_estimates = [] # μが既知の場合の推定量 T^2
S2_estimates = [] # μが未知の場合の推定量 S^2
# 各サンプルサイズでのシミュレーションの実行
for n in sample_sizes:
# 正規分布からサンプルを抽出
sample = np.random.normal(mu, sigma, n)
# μが既知の場合の最尤推定量 T^2
T2 = np.sum((sample - mu) ** 2) / n
# μが未知の場合の最尤推定量 S^2
sample_mean = np.mean(sample)
S2 = np.sum((sample - sample_mean) ** 2) / (n - 1)
# 推定量をリストに保存
T2_estimates.append(T2)
S2_estimates.append(S2)
# グラフの作成(理論値を追加)
plt.figure(figsize=(12, 8))
# μが既知の場合のプロット (緑)
plt.plot(sample_sizes, T2_estimates, marker='o', color='green', label='$T^2$ (μが既知の場合)', linestyle='--')
# μが未知の場合のプロット (オレンジ)
plt.plot(sample_sizes, S2_estimates, marker='x', color='orange', label='$S^2$ (μが未知の場合)', linestyle='--')
# 理論値の線を追加 (赤)
plt.axhline(y=true_variance, color='red', linestyle='-.', label='理論値: $\sigma^2$', linewidth=2)
# グラフの設定
plt.title('最尤推定量 $T^2$ と $S^2$ のサンプルサイズごとの結果')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('推定量')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()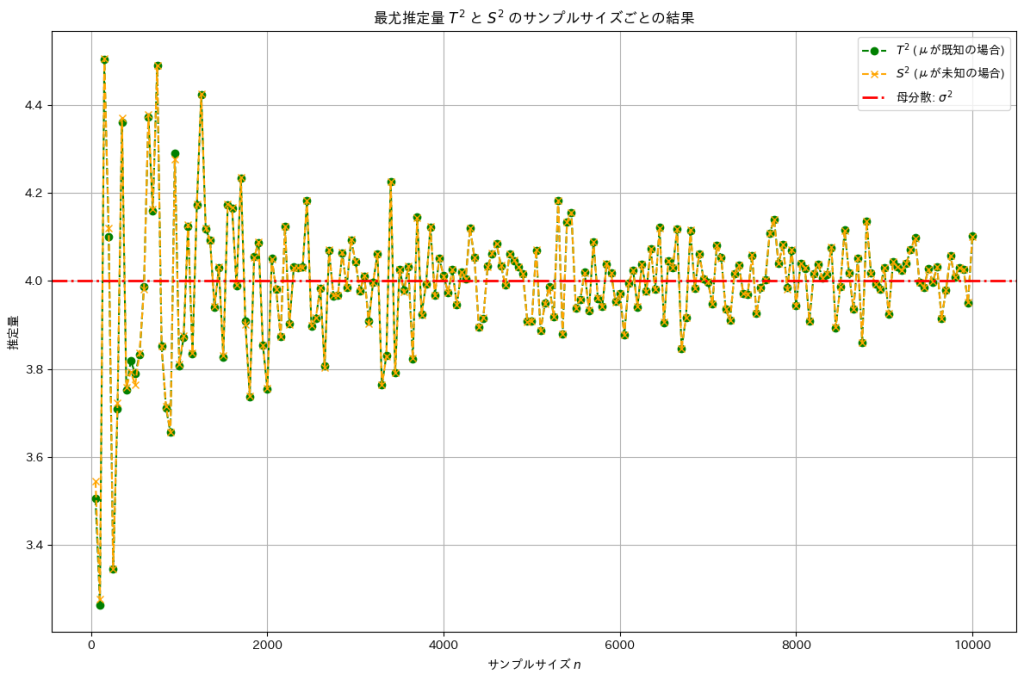
サンプルサイズを大きくすることで最尤推定量![]() と
と![]() は母分散
は母分散![]() に近づきました。
に近づきました。