不偏分散が母分散の不偏推定量であることを示しました。
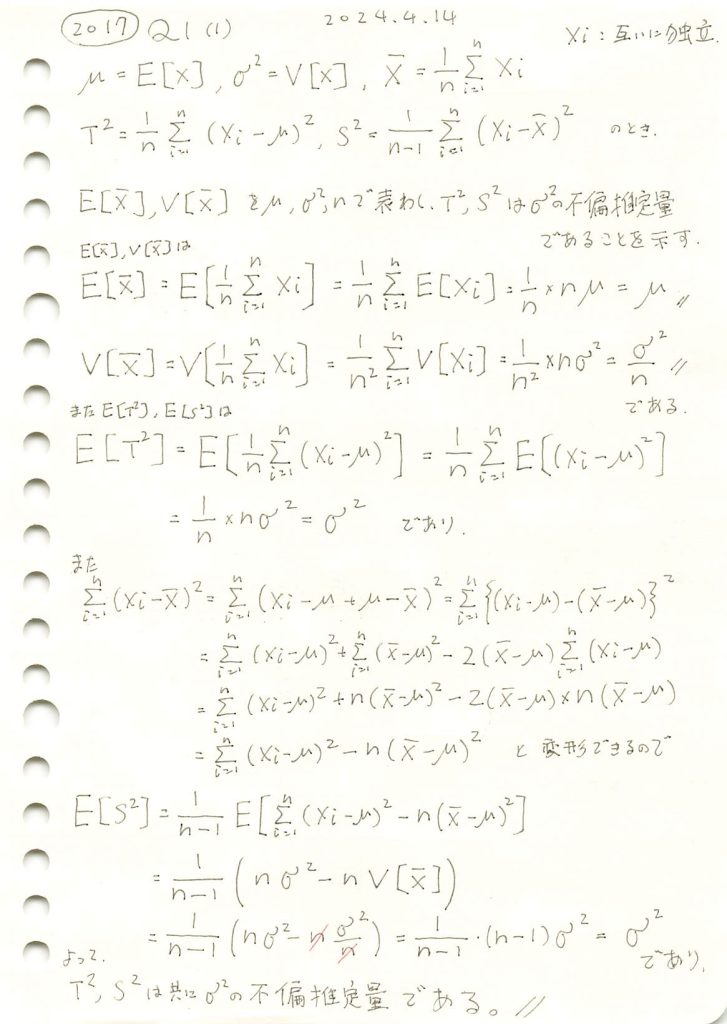
コード
サンプルサイズnを変化させて![]() ,
,![]() ,
,![]() ,
,![]() をそれぞれシミュレーションして描画します。
をそれぞれシミュレーションして描画します。
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
mu = 5.0 # 母平均
sigma = 2.0 # 母標準偏差
num_simulations = 1000 # シミュレーションの繰り返し回数
# n の範囲を設定 (100 から 10000 まで 100 刻み)
n_values = range(100, 10100, 100)
# 各 n に対する統計量を保存するリスト
E_X_bar_list = []
V_X_bar_list = []
E_T2_list = []
E_S2_list = []
# 各 n に対するシミュレーションの実行
for n in n_values:
sample_means = []
T2_values = []
S2_values = []
# シミュレーションの実行
for _ in range(num_simulations):
sample = np.random.normal(mu, sigma, n)
sample_mean = np.mean(sample)
sample_means.append(sample_mean)
# T^2 計算 (母平均使用)
T2 = np.mean((sample - mu) ** 2)
T2_values.append(T2)
# S^2 計算 (標本平均使用)
S2 = np.var(sample, ddof=1)
S2_values.append(S2)
# 結果をリストに保存
E_X_bar_list.append(np.mean(sample_means))
V_X_bar_list.append(np.var(sample_means))
E_T2_list.append(np.mean(T2_values))
E_S2_list.append(np.mean(S2_values))
# グラフの作成(理論値を追加)
plt.figure(figsize=(14, 10))
# 理論値
theoretical_mean = mu # E[X_bar] の理論値
theoretical_variance = sigma**2 / np.array(n_values) # V[X_bar] の理論値
theoretical_variance_true = sigma**2 # 母分散
# E[X_bar] のプロット
plt.subplot(2, 2, 1)
plt.plot(n_values, E_X_bar_list, marker='o', label='シミュレーション')
plt.axhline(y=theoretical_mean, color='r', linestyle='--', label='理論値: $E[\overline{X}] = \mu$')
plt.title('$E[\overline{X}]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$E[\overline{X}]$')
plt.legend()
# V[X_bar] のプロット
plt.subplot(2, 2, 2)
plt.plot(n_values, V_X_bar_list, marker='o', label='シミュレーション')
plt.plot(n_values, theoretical_variance, color='r', linestyle='--', label='理論値: $V[\overline{X}] = \\frac{\sigma^2}{n}$')
plt.title('$V[\overline{X}]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$V[\overline{X}]$')
plt.legend()
# E[T^2] のプロット
plt.subplot(2, 2, 3)
plt.plot(n_values, E_T2_list, marker='o', label='シミュレーション')
plt.axhline(y=theoretical_variance_true, color='r', linestyle='--', label='理論値: $E[T^2] = \sigma^2$')
plt.title('$E[T^2]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$E[T^2]$')
plt.legend()
# E[S^2] のプロット
plt.subplot(2, 2, 4)
plt.plot(n_values, E_S2_list, marker='o', label='シミュレーション')
plt.axhline(y=theoretical_variance_true, color='r', linestyle='--', label='理論値: $E[S^2] = \sigma^2$')
plt.title('$E[S^2]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$E[S^2]$')
plt.legend()
# グラフの表示
plt.tight_layout()
plt.show()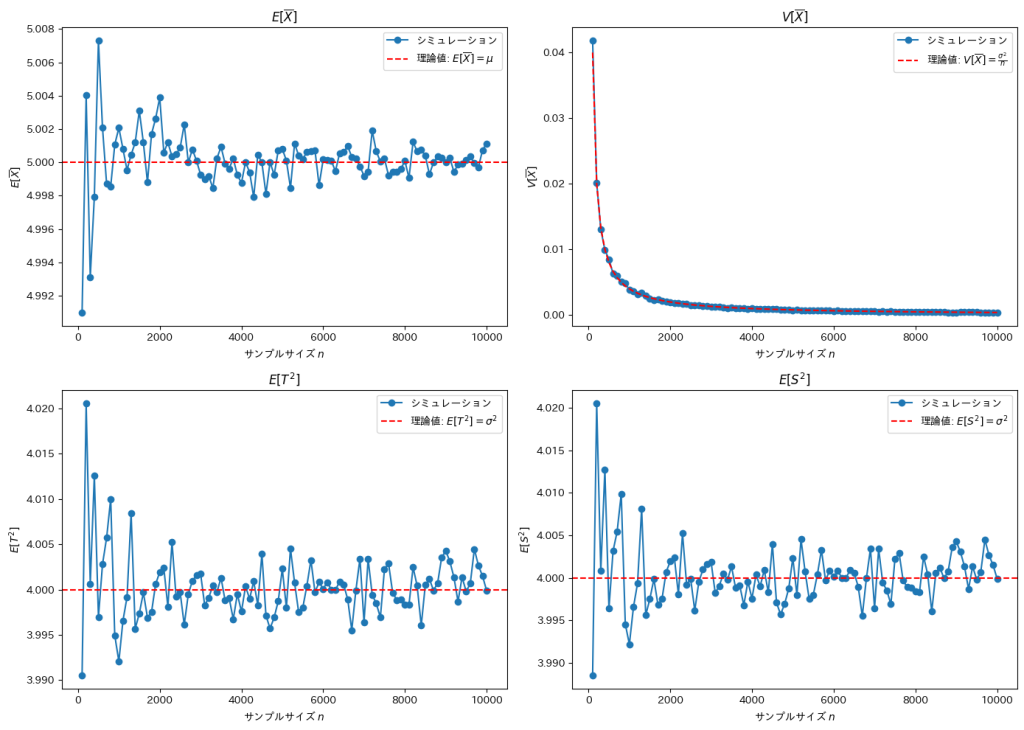
サンプルサイズnが増加するほど、各推定量は理論値に収束していく傾向に見えます。![]() と
と![]() は外れ値の影響を受けやすいため収束速度が緩やかです。
は外れ値の影響を受けやすいため収束速度が緩やかです。