MCAR性の検定統計量が与式になることを示しました。
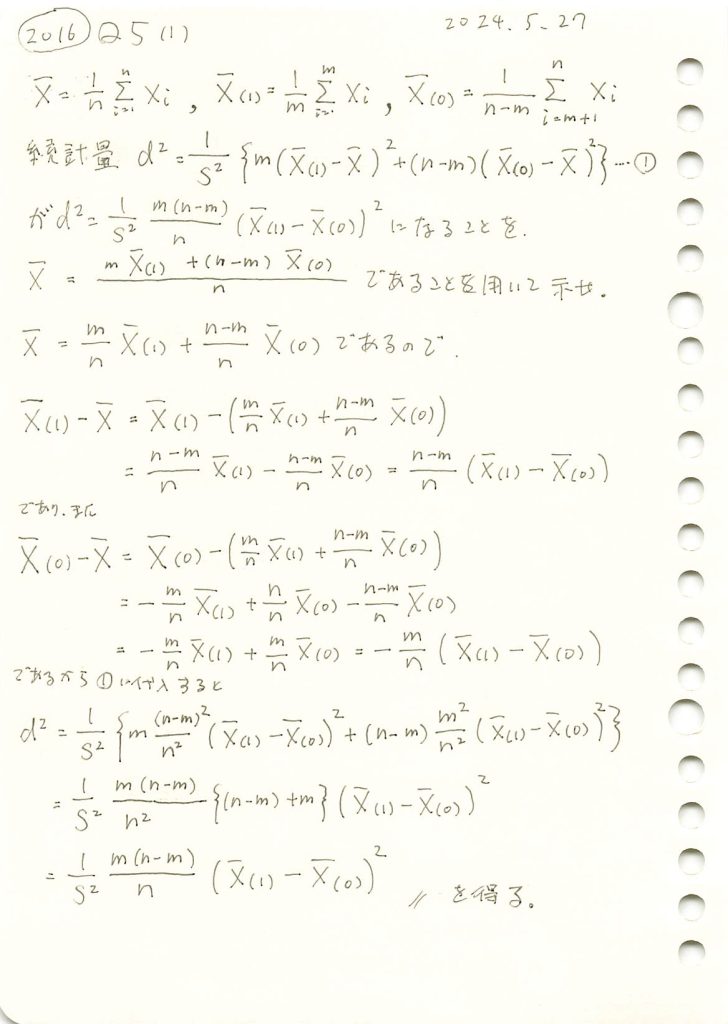
コード
二つの![]() が等価であるかシミュレーションによって検証してみます。
が等価であるかシミュレーションによって検証してみます。
# 2016 Q5(1) 2024.11.27
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 100 # 全体のサンプル数
m = 60 # 観測可能なデータのペア数
repeats = 10000 # シミュレーションの繰り返し回数
# Xのデータを正規分布に従ってランダムに生成
np.random.seed(42) # 乱数の再現性を確保
X = np.random.normal(loc=0, scale=1, size=n)
# データの欠損をシミュレート
X1 = X[:m] # 観測可能なXの値
X0 = X[m:] # Yが欠損しているXの値
# 理論的なd^2値を計算
S2 = np.var(X, ddof=1) # Xの標本不偏分散
X1_bar = np.mean(X1) # 観測可能なXの標本平均
X0_bar = np.mean(X0) # 欠損部分のXの標本平均
X_bar = np.mean(X) # 全体のXの標本平均
# d^2の直接計算
d2_direct = (1 / S2) * (m * (X1_bar - X_bar)**2 + (n - m) * (X0_bar - X_bar)**2)
# d^2の簡略化された計算
d2_simplified = (1 / S2) * (m * (n - m) / n) * (X1_bar - X0_bar)**2
# シミュレーションを実行して比較
d2_direct_simulations = []
d2_simplified_simulations = []
for _ in range(repeats):
# Xを再生成してランダムサンプリングをシミュレート
X = np.random.normal(loc=0, scale=1, size=n)
X1 = X[:m]
X0 = X[m:]
# 各種統計量を再計算
S2 = np.var(X, ddof=1)
X1_bar = np.mean(X1)
X0_bar = np.mean(X0)
X_bar = np.mean(X)
# d^2値を計算してリストに格納
d2_direct_simulations.append((1 / S2) * (m * (X1_bar - X_bar)**2 + (n - m) * (X0_bar - X_bar)**2))
d2_simplified_simulations.append((1 / S2) * (m * (n - m) / n) * (X1_bar - X0_bar)**2)
# 平均絶対差を計算
mean_absolute_difference = np.mean(np.abs(np.array(d2_direct_simulations) - np.array(d2_simplified_simulations)))
# 計算結果を出力
print(f"シミュレーションによるd^2 の平均絶対差: {mean_absolute_difference:.2e}")
# 数式を含む散布図をプロット
plt.figure(figsize=(8, 6))
plt.scatter(d2_direct_simulations, d2_simplified_simulations, alpha=0.5, s=10, label="シミュレーション結果")
plt.plot([min(d2_direct_simulations), max(d2_direct_simulations)],
[min(d2_direct_simulations), max(d2_direct_simulations)], 'r--', label="$y=x$") # y=xの基準線
plt.title("$d^2$ の二式の比較", fontsize=14)
plt.xlabel(r"$d^2 = \frac{1}{S^2} \left[ m(\overline{X}_{(1)} - \overline{X})^2 + (n-m)(\overline{X}_{(0)} - \overline{X})^2 \right]$", fontsize=12)
plt.ylabel(r"$d^2 = \frac{1}{S^2} \cdot \frac{m(n-m)}{n} \cdot (\overline{X}_{(1)} - \overline{X}_{(0)})^2$", fontsize=12)
plt.legend(fontsize=12) # 凡例を追加
plt.grid(alpha=0.3) # グリッドを薄く表示
plt.show()シミュレーションによるd^2 の平均絶対差: 1.26e-16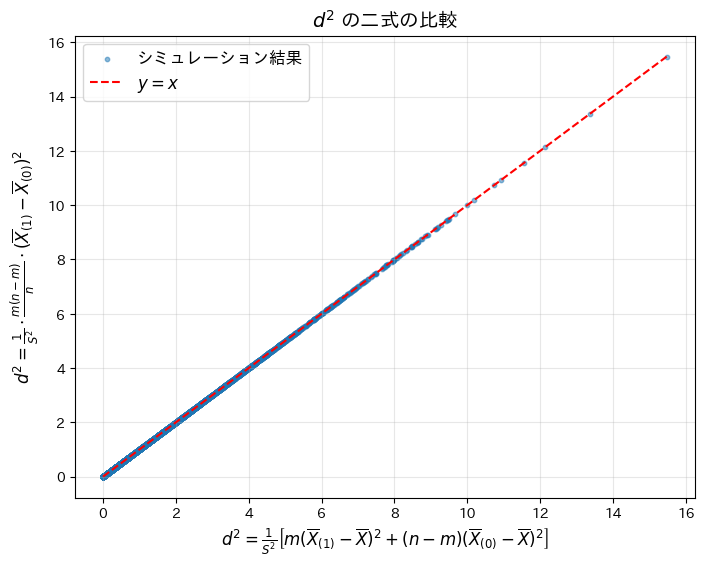
二つの![]() が等価であることがシミュレーションによって確認されました。なお、平均絶対差が僅かに生じたのは、浮動小数点演算による誤差であると考えられます。
が等価であることがシミュレーションによって確認されました。なお、平均絶対差が僅かに生じたのは、浮動小数点演算による誤差であると考えられます。