n個の標準正規分布に従う乱数が0以上1以下となる個数が従う分布を求めました。また乱数が0以上1以下となる確率の推定値の分散を求めました。

コード
この実験では、標準正規分布N(0,1)と、n個の標準正規分布に従う乱数のうち0以上1以下となる個数Xの分布、およびその確率を推定する量![]() の分布を確認します。
の分布を確認します。
# 2016 Q4(1) 2024.11.23
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, norm
# ---- グラフ 1: 標準正規分布 N(0,1) と範囲 (0 < Z < 1) ----
# パラメータの設定
n_samples = 10000 # サンプル数
z_min, z_max = 0, 1 # 条件の範囲 (0 < Z < 1)
# 標準正規分布 N(0,1) に従う乱数を生成します
samples = np.random.normal(0, 1, n_samples)
# 理論的な標準正規分布の確率密度関数を計算します
x1 = np.linspace(-4, 4, 500)
pdf_theoretical = norm.pdf(x1, loc=0, scale=1)
# ---- グラフ 2: X の分布(二項分布) ----
# シミュレーションの設定
n_trials = 1000 # シミュレーションの試行回数
n = 50 # サンプルサイズ (1試行あたりの乱数生成数)
theta = 0.3413 # 真の成功確率 (0 < Z < 1)
# X の分布を計算
X_values = []
for _ in range(n_trials):
samples_trial = np.random.normal(0, 1, n)
X = np.sum((samples_trial > z_min) & (samples_trial < z_max))
X_values.append(X)
# 理論的な二項分布
x2 = np.arange(0, n + 1)
binomial_pmf = binom.pmf(x2, n, theta)
# ---- グラフ 3: θ̂1 の分布と理論分布 ----
# θ̂1 = X / n を計算
theta_hat_1_values = [X / n for X in X_values]
# 理論分布用のデータ
x3 = np.linspace(0, 1, 100)
binomial_pdf = norm.pdf(x3, loc=theta, scale=np.sqrt(theta * (1 - theta) / n))
# ---- 3つのグラフを描画 ----
plt.figure(figsize=(10, 10)) # グラフ全体のサイズを指定
# グラフ 1
plt.subplot(3, 1, 1)
plt.hist(samples, bins=50, density=True, alpha=0.5, label='全データ (N(0,1))', color='purple')
plt.axvspan(z_min, z_max, color='orange', alpha=0.3, label='0 < Z < 1 の領域')
plt.plot(x1, pdf_theoretical, 'r-', label='理論分布 (N(0,1))', linewidth=2)
plt.title('N(0,1) に従う乱数のヒストグラムと領域', fontsize=14)
plt.xlabel('Z 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフ 2
plt.subplot(3, 1, 2)
plt.hist(X_values, bins=np.arange(0, n + 2) - 0.5, density=True, alpha=0.6, color='green', label='X の分布 (シミュレーション)')
plt.plot(x2, binomial_pmf, 'ro-', label='理論分布 (Binomial)', markersize=4)
plt.title('X の分布と理論分布の比較', fontsize=14)
plt.xlabel('X 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフ 3
plt.subplot(3, 1, 3)
plt.hist(theta_hat_1_values, bins=10, density=True, alpha=0.6, color='blue', label='$\\hat{\\theta}_1$ の分布 (シミュレーション)')
plt.plot(x3, binomial_pdf, 'r-', label='理論分布 $N(\\theta, V[\\hat{\\theta}_1])$', linewidth=2)
plt.title('$\\hat{\\theta}_1$ の分布と理論分布の比較', fontsize=14)
plt.xlabel('$\\hat{\\theta}_1$ 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフを表示
plt.tight_layout() # 全体を整える
plt.show()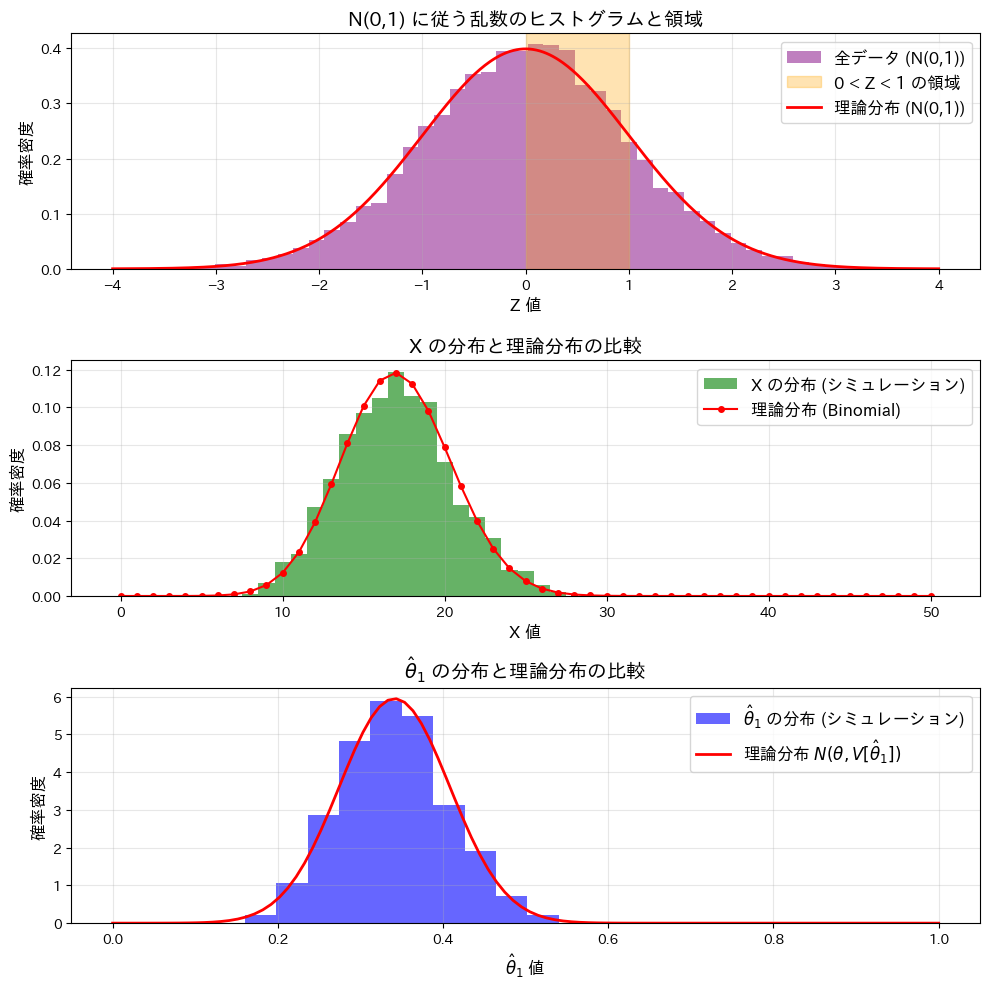
この実験によってXが二項分布B(n,θ)に従うことと、![]() が正規分布
が正規分布![]() に従うことが確認できました。
に従うことが確認できました。