指数分布の和がガンマ分布になることを示しました。

コード
指数分布に従う確率変数X1~Xnの和がガンマ分布に従うのをかを確かめるため、シミュレーションを行いました。この実験では、まずn=5の場合について確かめました。
# 2016 Q2(4) 2024.11.18
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # 真のλ
n = 5 # 指数分布の和の数 (ガンマ分布の形状パラメータ)
sample_size = 10000 # シミュレーションのサンプルサイズ
# 1. 指数分布の和をシミュレーション
sum_of_exponentials = np.sum(np.random.exponential(scale=1/lambda_value, size=(sample_size, n)), axis=1)
# 2. ガンマ分布の理論値を計算
x = np.linspace(0, max(sum_of_exponentials), 1000)
gamma_pdf = gamma.pdf(x, a=n, scale=1/lambda_value)
# 3. ヒストグラムと理論的なガンマ分布をプロット
plt.figure(figsize=(10, 6))
plt.hist(sum_of_exponentials, bins=50, density=True, alpha=0.6, color='skyblue', label='シミュレーション (指数分布の和)')
plt.plot(x, gamma_pdf, 'r-', label='理論的なガンマ分布', linewidth=2)
# グラフの設定
plt.title('指数分布の和 (n=5) とガンマ分布の比較', fontsize=16)
plt.xlabel('値', fontsize=14)
plt.ylabel('密度', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
# プロット表示
plt.show()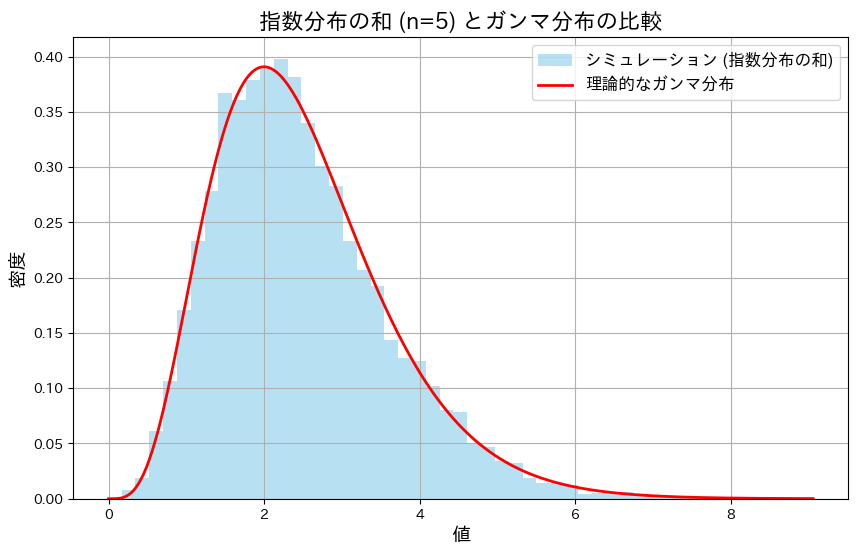
5つの指数分布の和は、形状パラメータが5のガンマ分布に一致することが確認できました。
次に、nを変化させてシミュレーションを行い、分布の形状の変化を観察します。また、それらの分布がガンマ分布と一致するかを確認します。
# 2016 Q2(4) 2024.11.18
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # 真のλ
n_values = [2, 5, 10, 20] # nの値を変化させる
sample_size = 10000 # シミュレーションのサンプルサイズ
# 2x2のグリッドでプロット
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.flatten()
for i, n in enumerate(n_values):
# 指数分布の和をシミュレーション
sum_of_exponentials = np.sum(np.random.exponential(scale=1/lambda_value, size=(sample_size, n)), axis=1)
# ガンマ分布の理論値を計算
x = np.linspace(0, 20, 1000) # 横軸の範囲を0~20に設定
gamma_pdf = gamma.pdf(x, a=n, scale=1/lambda_value)
# ヒストグラムと理論的なガンマ分布をプロット
ax = axes[i]
ax.hist(sum_of_exponentials, bins=50, range=(0, 20), density=True, alpha=0.6, color='skyblue', label='シミュレーション (指数分布の和)')
ax.plot(x, gamma_pdf, 'r-', label='理論的なガンマ分布', linewidth=2)
# グラフの設定
ax.set_title(f'n={n}', fontsize=14)
ax.set_xlabel('値', fontsize=12)
ax.set_ylabel('密度', fontsize=12)
ax.legend(fontsize=10)
ax.grid(True)
# 全体のレイアウト調整
plt.suptitle('nを変化させた指数分布の和とガンマ分布の比較', fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()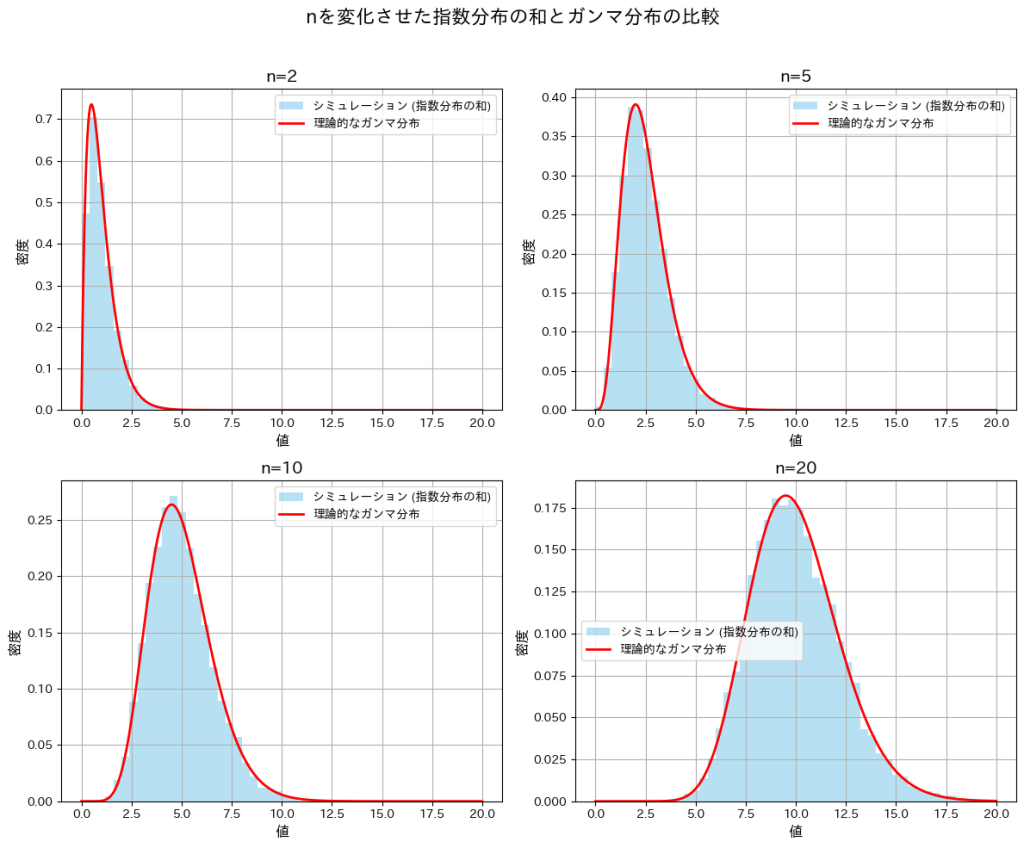
nが小さいときは分布が右に裾が長くなり、nが大きくなるにつれて左右対称に近づいています。また、どのnにおいても形状パラメータnのガンマ分布とよく一致していることが確認できました。