指数分布のλと、上側α点を返す関数の最尤推定量を求め、不偏であるか確認しました。

コード
最尤推定量![]() をシミュレーションし、理論値
をシミュレーションし、理論値![]() と比較します。共にグラフに描画し、どの程度一致しているか確認します。
と比較します。共にグラフに描画し、どの程度一致しているか確認します。
# 2016 Q2(3) 2024.11.17
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_value = 2 # 真のλ
n = 100 # サンプル数
c = 1.0 # Q(c) を計算するための c の値
alpha_values = [0.1, 0.25, 0.5, 0.75, 0.9] # αの値
# 1. 指数分布からサンプルを生成
samples = np.random.exponential(scale=1/lambda_value, size=n)
# 2. λの最尤推定量を計算
lambda_hat = n / np.sum(samples)
# 3. Q(c) の最尤推定量を計算
Q_hat_c = np.exp(-lambda_hat * c)
Q_theoretical_c = np.exp(-lambda_value * c)
# 4. u(α) の最尤推定量を計算
u_hat_alpha = [-np.mean(samples) * np.log(alpha) for alpha in alpha_values]
u_theoretical_alpha = [-np.log(alpha) / lambda_value for alpha in alpha_values]
# グラフ作成部分
plt.figure(figsize=(10, 6))
# 理論値と最尤推定量の u(α) をプロット
plt.plot(alpha_values, u_theoretical_alpha, 'r-o', label='u(α) 理論値', linewidth=2)
plt.plot(alpha_values, u_hat_alpha, 'b--s', label='u(α) 最尤推定量', linewidth=2) # 'b--s' で破線とマーカーを指定
# グラフの設定
plt.title('u(α) の理論値と最尤推定量の比較', fontsize=16)
plt.xlabel('α', fontsize=14)
plt.ylabel('u(α)', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.xticks(alpha_values)
# グラフの表示
plt.show()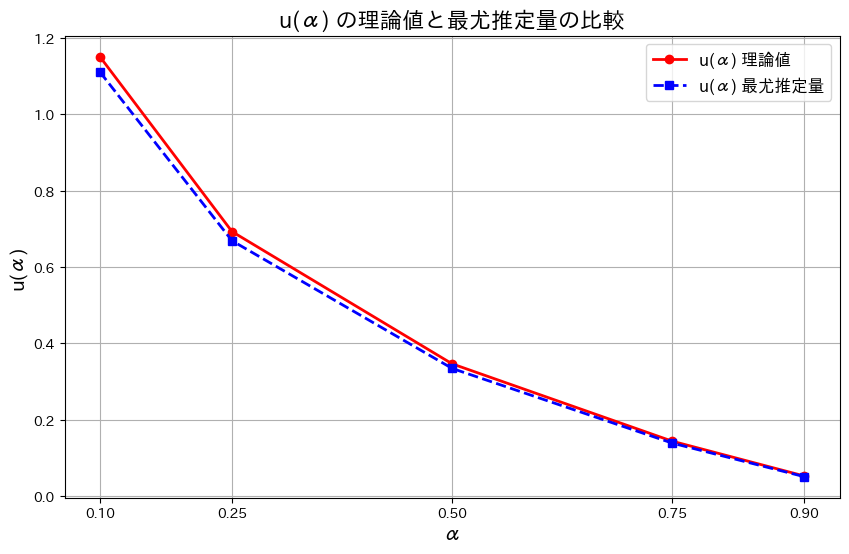
![]() はわずかに誤差があるものの概ね一致しました。また誤差はαが大きくなるにつれて小さくなります。その理由は、αが大きくなるとu(α)の値が小さくなり、分布の高密度な部分にサンプルが集中するためと考えられます。
はわずかに誤差があるものの概ね一致しました。また誤差はαが大きくなるにつれて小さくなります。その理由は、αが大きくなるとu(α)の値が小さくなり、分布の高密度な部分にサンプルが集中するためと考えられます。