指数分布の上側α点を返す関数を求めました。

コード
パラメータλ=2の指数分布において、Q(c)=P(X>c)をシミュレーションによって求め、理論値と比較します。c=1とします。また、P(X>u(α))=αとなるu(α)も同様に比較します。
# 2016 Q2(2) 2024.11.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_value = 2 # λの値
sample_size = 10000 # シミュレーションに使用するサンプル数
c = 1.0 # 上側確率を計算するための定数 c
alpha_values = [0.1, 0.25, 0.5, 0.75, 0.9] # 上側 100α% 点を確認する α の値
# 1. 上側確率 Q(c) のシミュレーション
random_samples = np.random.exponential(scale=1/lambda_value, size=sample_size)
empirical_prob_c = np.mean(random_samples > c) # シミュレーションによる上側確率
theoretical_prob_c = np.exp(-lambda_value * c) # 理論的な上側確率
# 結果表示
print("上側確率 Q(c) のシミュレーション結果")
print(f"理論的な Q(c) = {theoretical_prob_c:.4f}")
print(f"シミュレーションによる Q(c) = {empirical_prob_c:.4f}\n")
# 2. 上側 100α% 点 u(α) の確認
alpha_results = []
for alpha in alpha_values:
u_alpha = -np.log(alpha) / lambda_value # 理論的な上側 100α% 点
empirical_prob_alpha = np.mean(random_samples > u_alpha) # u(α) を超える割合
alpha_results.append((alpha, u_alpha, empirical_prob_alpha))
# 結果表示
print("上側 100α% 点 u(α) のシミュレーション結果")
for alpha, u_alpha, empirical_prob_alpha in alpha_results:
print(f"α = {alpha:.2f} | 理論的な u(α) = {u_alpha:.4f} | 理論的確率P(X>u(α)) = {alpha:.2f} | シミュレーション確率 = {empirical_prob_alpha:.4f}")
# ヒストグラムのプロット
plt.figure(figsize=(10, 6))
plt.hist(random_samples, bins=50, density=True, alpha=0.6, color='skyblue', label='サンプルのヒストグラム')
# 理論的な確率密度関数
x = np.linspace(0, max(random_samples), 1000)
theoretical_pdf = lambda_value * np.exp(-lambda_value * x)
plt.plot(x, theoretical_pdf, 'r-', label='理論的な確率密度関数', linewidth=2)
# 上側 100α% 点 u(α) のプロット
for alpha, u_alpha, _ in alpha_results:
plt.axvline(u_alpha, linestyle='dashed', label=f'u({alpha}) = {u_alpha:.2f}')
# グラフ設定
plt.title(f'指数分布 Exp({lambda_value}) のシミュレーションと理論分布')
plt.xlabel('x')
plt.ylabel('密度')
plt.legend(fontsize=10)
plt.grid(True)
# プロット表示
plt.show()上側確率 Q(c) のシミュレーション結果
理論的な Q(c) = 0.1353
シミュレーションによる Q(c) = 0.1365
上側 100α% 点 u(α) のシミュレーション結果
α = 0.10 | 理論的な u(α) = 1.1513 | 理論的確率P(X>u(α)) = 0.10 | シミュレーション確率 = 0.1035
α = 0.25 | 理論的な u(α) = 0.6931 | 理論的確率P(X>u(α)) = 0.25 | シミュレーション確率 = 0.2480
α = 0.50 | 理論的な u(α) = 0.3466 | 理論的確率P(X>u(α)) = 0.50 | シミュレーション確率 = 0.4962
α = 0.75 | 理論的な u(α) = 0.1438 | 理論的確率P(X>u(α)) = 0.75 | シミュレーション確率 = 0.7513
α = 0.90 | 理論的な u(α) = 0.0527 | 理論的確率P(X>u(α)) = 0.90 | シミュレーション確率 = 0.9011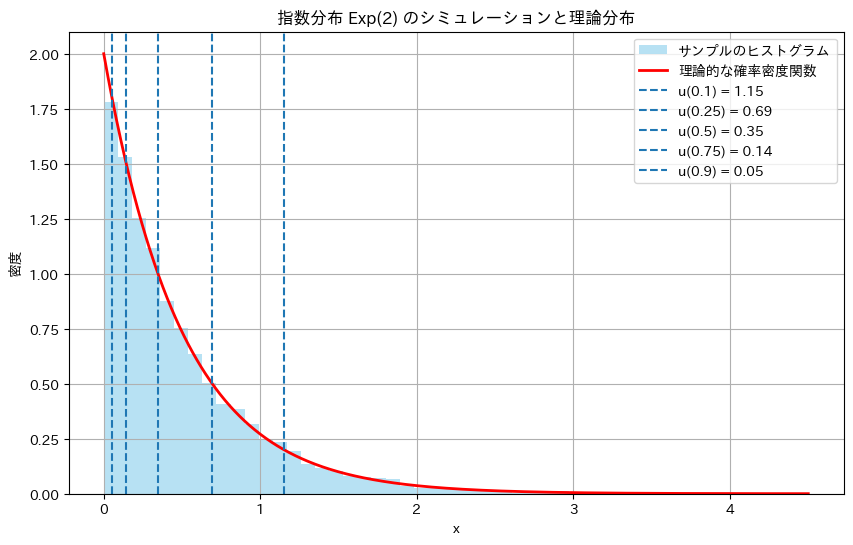
Q(c)=P(X>c)とP(X>u(α))の理論値とシミュレーション結果は非常によく一致しました。