正規分布の母平均μに対してθ=exp(μ)をパラメータとする尤度関数からフィッシャー情報量を求め、その逆数が不偏推定量の分散と一致するか否かを確かめた。
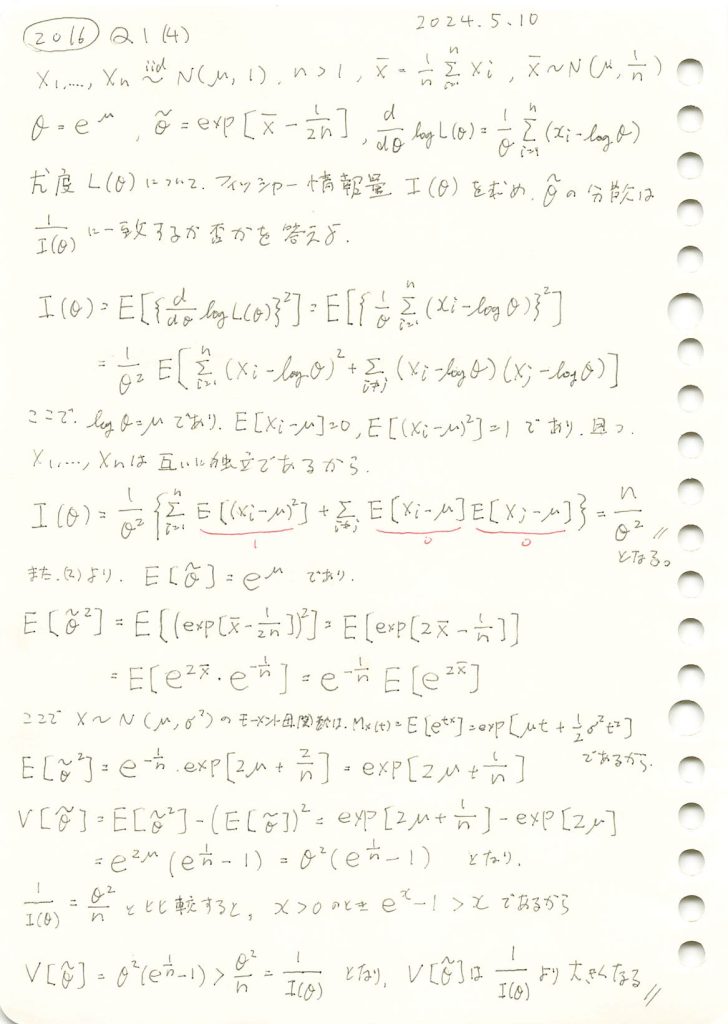
コード
![]() となることを確認するために、両辺をグラフで比較してみます。
となることを確認するために、両辺をグラフで比較してみます。
# 2016 Q1(4) 2024.11.14
import numpy as np
import matplotlib.pyplot as plt
# θ の範囲設定
theta_values = np.linspace(0.1, 5.0, 10) # 0.1から5.0までの範囲で計算
n_samples = 50 # サンプルサイズ
# 分散 V[θ~] と 1/I(θ) の計算
V_theta_tilde = theta_values**2 * (np.exp(1 / n_samples) - 1)
Fisher_info_inverse = theta_values**2 / n_samples # 1 / I(θ)
# 折れ線グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(theta_values, V_theta_tilde, label=r'$V[\tilde{\theta}]$ (不偏推定量の分散)', color='blue', linestyle='-', marker='o')
plt.plot(theta_values, Fisher_info_inverse, label=r'$1/I(\theta)$ (フィッシャー情報量の逆数)', color='red', linestyle='--', marker='s')
plt.title('不偏推定量の分散とフィッシャー情報量の逆数の比較', fontsize=16)
plt.xlabel(r'$\theta$', fontsize=14)
plt.ylabel('分散', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()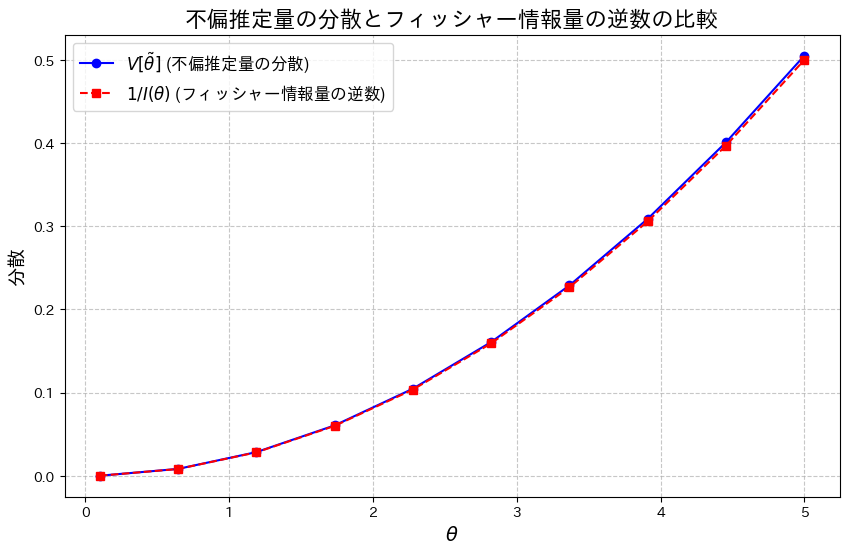
わずかに![]() となっているようです。
となっているようです。
次に、2式の差![]() をプロットし、その差を確認してみます。
をプロットし、その差を確認してみます。
# 2016 Q1(4) 2024.11.14
import numpy as np
import matplotlib.pyplot as plt
# θ の範囲設定
theta_values = np.linspace(0.1, 5.0, 10) # 0.1から5.0までの範囲で計算
n_samples = 50 # サンプルサイズ
# 分散 V[θ~] と 1/I(θ) の計算
V_theta_tilde = theta_values**2 * (np.exp(1 / n_samples) - 1)
Fisher_info_inverse = theta_values**2 / n_samples # 1 / I(θ)
# V[θ~] - 1/I(θ) を計算
diff_V_Fisher = V_theta_tilde - Fisher_info_inverse
# 差分をプロット
plt.figure(figsize=(10, 6))
plt.plot(theta_values, diff_V_Fisher, color='purple', linestyle='-', marker='o', label=r'$V[\tilde{\theta}] - \frac{1}{I(\theta)}$')
plt.title('不偏推定量の分散とフィッシャー情報量逆数の差', fontsize=16)
plt.xlabel(r'$\theta$', fontsize=14)
plt.ylabel(r'$V[\tilde{\theta}] - \frac{1}{I(\theta)}$', fontsize=14)
plt.axhline(0, color='black', linestyle='--', linewidth=1) # y=0 の線を追加
plt.legend(fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()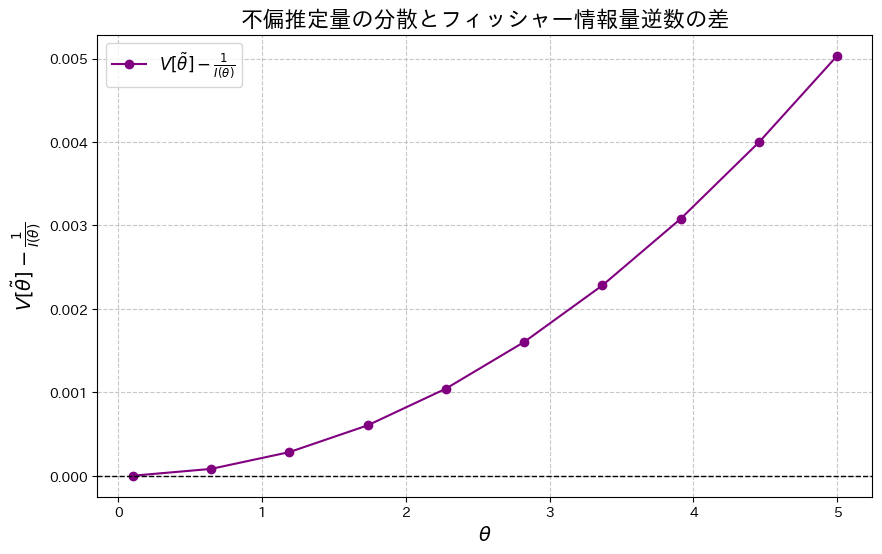
2式の差![]() が存在することが確認できました。この差は、θが増加するにつれて大きくなる傾向が見られます。
が存在することが確認できました。この差は、θが増加するにつれて大きくなる傾向が見られます。
次に、乱数を用いたシミュレーションを行い、![]() を重ねてプロットしてみます。
を重ねてプロットしてみます。
# 2016 Q1(4) 2024.11.14
import numpy as np
import matplotlib.pyplot as plt
# 再定義:thetaの範囲
theta_values = np.linspace(0.1, 5.0, 100)
n_samples = 50
n_trials = 10000 # シミュレーション試行回数
# 理論分散 V[θ~] と 1/I(θ) の計算
V_theta_tilde = theta_values**2 * (np.exp(1 / n_samples) - 1)
Fisher_info_inverse = theta_values**2 / n_samples
# シミュレーションによる分散の再計算
simulated_V_theta_tilde = []
for theta in theta_values:
mse_trials = []
for _ in range(n_trials):
sample = np.random.normal(loc=np.log(theta), scale=1, size=n_samples) # 平均 log(theta), 分散 1
X_bar = np.mean(sample)
theta_tilde = np.exp(X_bar - 1 / (2 * n_samples)) # 不偏推定量
mse_trials.append((theta_tilde - theta)**2) # 二乗誤差
simulated_var = np.mean(mse_trials) # シミュレーションによる分散 (MSE)
simulated_V_theta_tilde.append(simulated_var)
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(theta_values, V_theta_tilde, label='理論分散 $V[\\tilde{\\theta}]$', linestyle='-', color='blue', alpha=0.7)
plt.scatter(theta_values, simulated_V_theta_tilde, label='シミュレーション分散 $V[\\tilde{\\theta}]$', marker='s', color='red', alpha=0.6)
plt.plot(theta_values, Fisher_info_inverse, label='$1/I(\\theta)$ (フィッシャー情報量の逆数)', linestyle='--', color='green', alpha=0.8)
plt.title('不偏推定量の分散とフィッシャー情報量の逆数の比較', fontsize=16)
plt.xlabel('$\\theta$', fontsize=14)
plt.ylabel('分散', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()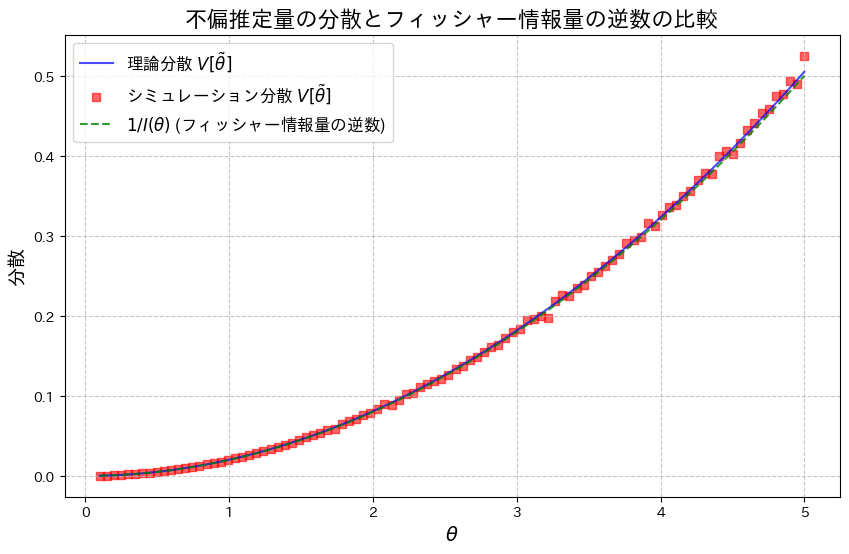
![]() は、わずかに
は、わずかに![]() を下回る場合があるようです。これは、シミュレーションにおける乱数の誤差によるものだと考えられます。
を下回る場合があるようです。これは、シミュレーションにおける乱数の誤差によるものだと考えられます。