正規分布の母平均μに対するθ=exp(μ)の最尤推定量の平均二乗誤差が0になることを示しました。

コード
シミュレーションを行います。![]() に対して、
に対して、![]() を計算し、理論値とともにプロットします。サンプルサイズnを増加させて、MSEの変化を観察します。
を計算し、理論値とともにプロットします。サンプルサイズnを増加させて、MSEの変化を観察します。
# 2016 Q1(3) 2024.11.13
import numpy as np
import matplotlib.pyplot as plt
# 真の値とシミュレーション設定
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の θ = e^mu
n_trials = 10000 # シミュレーション試行回数
sample_sizes = np.arange(5, 101, 5) # サンプルサイズの範囲
# MSEを格納するリスト
mse_simulated = []
# 理論的なMSEの計算関数
def theoretical_mse(n, mu):
return np.exp(2 * mu) * (np.exp(2 / n) - 2 * np.exp(1 / (2 * n)) + 1)
mse_theoretical = [theoretical_mse(n, mu_true) for n in sample_sizes]
# シミュレーションでのMSE計算
for n_samples in sample_sizes:
mse_trials = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1, size=n_samples)
X_bar = np.mean(sample)
theta_hat = np.exp(X_bar) # 最尤推定量
mse_trials.append((theta_hat - theta_true) ** 2) # MSEの計算
mse_simulated.append(np.mean(mse_trials)) # 試行平均を格納
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, mse_simulated, marker='o', linestyle='-', color='blue', label='シミュレーション MSE')
plt.plot(sample_sizes, mse_theoretical, marker='s', linestyle='--', color='red', label='理論的 MSE')
plt.title('MSEのシミュレーションと理論値', fontsize=16)
plt.xlabel('サンプルサイズ $n$', fontsize=14)
plt.ylabel('MSE', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.show()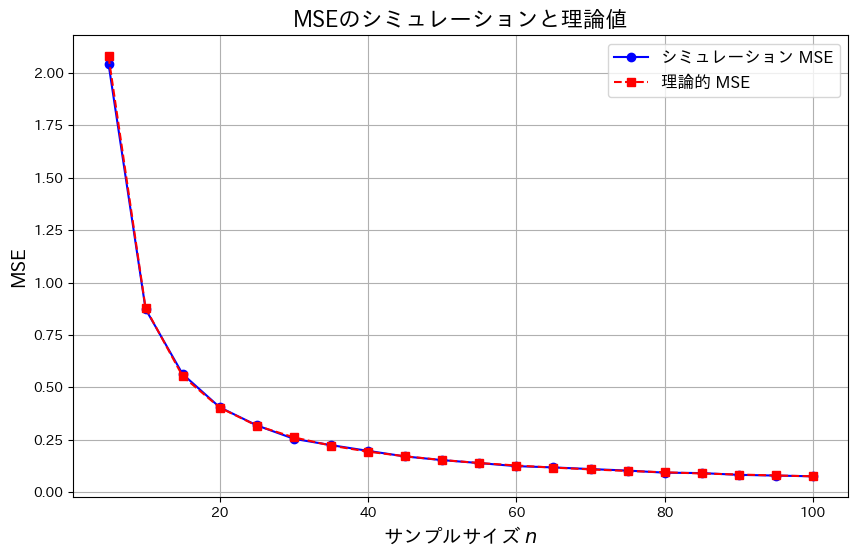
サンプルサイズnが増加するにつれて、![]() は0に近づきました。これにより、
は0に近づきました。これにより、![]() になることが理論とシミュレーションの両方で確認できました。また、この結果から最尤推定量
になることが理論とシミュレーションの両方で確認できました。また、この結果から最尤推定量 ![]() が漸近的一致性を持つことが分かりました。
が漸近的一致性を持つことが分かりました。