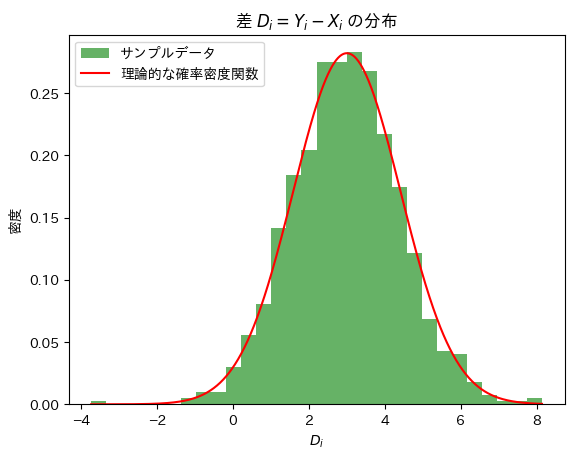
正規分布の差の分布を求める問題をやりました。

コード
シミュレーションによる計算
# 2022 Q4(5) 2024.8.13
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# パラメータの設定
mu_i = 5.0 # 平均値 mu_i
theta = 3.0 # シフトパラメータ θ
sigma = 1.0 # 標準偏差 σ
n = 1000 # サンプル数
# X_i と Y_i のサンプル生成
X_i = np.random.normal(mu_i, sigma, n)
Y_i = np.random.normal(mu_i + theta, sigma, n)
# D_i の計算
D_i = Y_i - X_i
# シミュレーション結果の平均と分散を計算
mean_simulation = np.mean(D_i)
variance_simulation = np.var(D_i)
# 理論上の平均と分散
mean_theoretical = theta
variance_theoretical = 2 * sigma**2
# 結果の表示
print(f"シミュレーション結果: 平均 = {mean_simulation}, 分散 = {variance_simulation}")
print(f"理論値: 平均 = {mean_theoretical}, 分散 = {variance_theoretical}")
# サンプルのヒストグラムを作成
plt.hist(D_i, bins=30, density=True, alpha=0.6, color='g', label='サンプルデータ')
# 理論上の分布を重ねる
x = np.linspace(min(D_i), max(D_i), 1000)
plt.plot(x, stats.norm.pdf(x, mean_theoretical, np.sqrt(variance_theoretical)), 'r', label='理論的な確率密度関数')
plt.title("差 $D_i = Y_i - X_i$ の分布")
plt.xlabel("$D_i$")
plt.ylabel("密度")
plt.legend()
plt.show()シミュレーション結果: 平均 = 2.975536685240219, 分散 = 2.005575154363111
理論値: 平均 = 3.0, 分散 = 2.0