対数で変数変換した場合の分布を求めました。
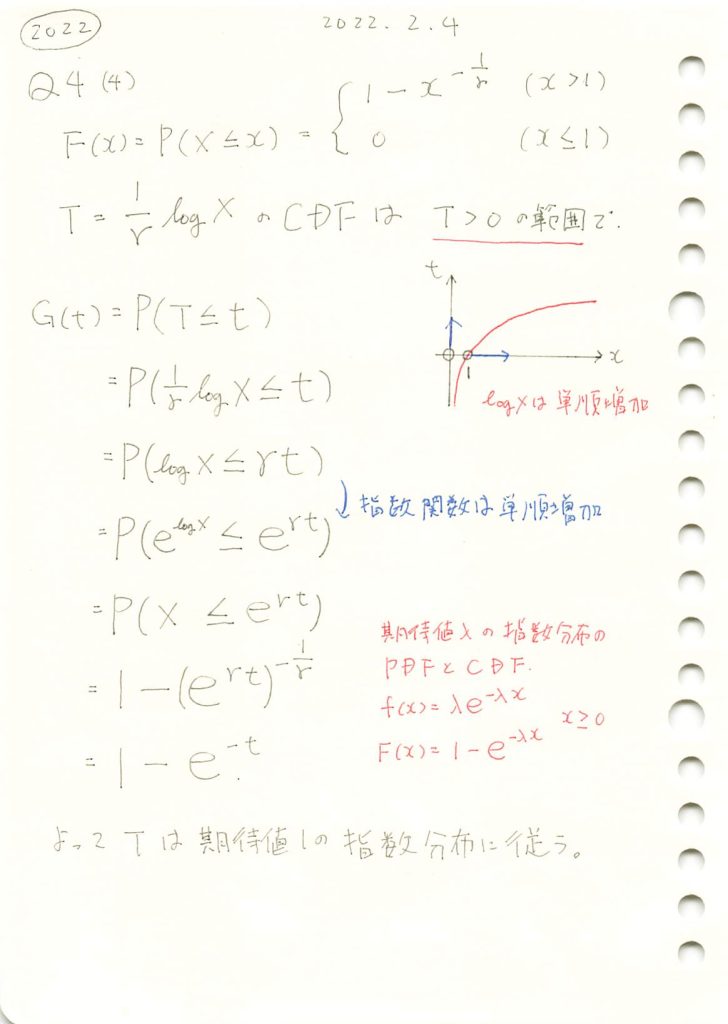
コード
数式を使った計算
# 2022 Q4(4) 2024.8.11
import sympy as sp
# シンボリック変数の定義
t, gamma = sp.symbols('t gamma', positive=True)
x = sp.symbols('x', real=True, positive=True)
# 累積分布関数 F_X(x) の定義
F_X = sp.Piecewise((0, x <= 1), (1 - x**(-1/gamma), x > 1))
# F_T(t) の計算
F_T = F_X.subs(x, sp.exp(gamma * t))
# f_T(t) の計算(F_T(t) を t で微分)
f_T = sp.diff(F_T, t)
# 結果の表示
display(F_T, f_T)
# LaTeXで表示できなときは、こちら
#sp.pprint(F_T, use_unicode=True)
#sp.pprint(f_T, use_unicode=True)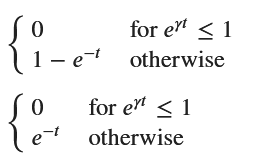
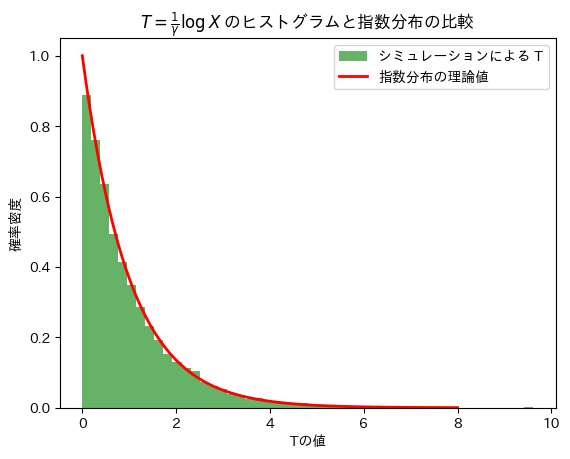
シミュレーションによる計算
# 2022 Q4(4) 2024.8.11
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# パラメータ設定
gamma = 1.0 # γの値(例えば1)
num_samples = 10000 # サンプルサイズ
# 累積分布関数 F(x) に従う乱数を生成
X = (np.random.uniform(size=num_samples))**(-gamma)
# T = (1/γ) * log(X) の計算
T = (1/gamma) * np.log(X)
# ヒストグラムをプロット
plt.hist(T, bins=50, density=True, alpha=0.6, color='g', label="シミュレーションによる T")
# 理論的な指数分布の密度関数をプロット
x = np.linspace(0, 8, 100)
pdf = stats.expon.pdf(x) # 指数分布(λ=1)の密度関数
plt.plot(x, pdf, 'r-', lw=2, label='指数分布の理論値')
# グラフの設定(日本語でキャプションとラベルを設定)
plt.xlabel('Tの値')
plt.ylabel('確率密度')
plt.title(r'$T = \frac{1}{\gamma} \log X$ のヒストグラムと指数分布の比較')
plt.legend()
plt.show()