とある分布の期待値と分散を求めました。
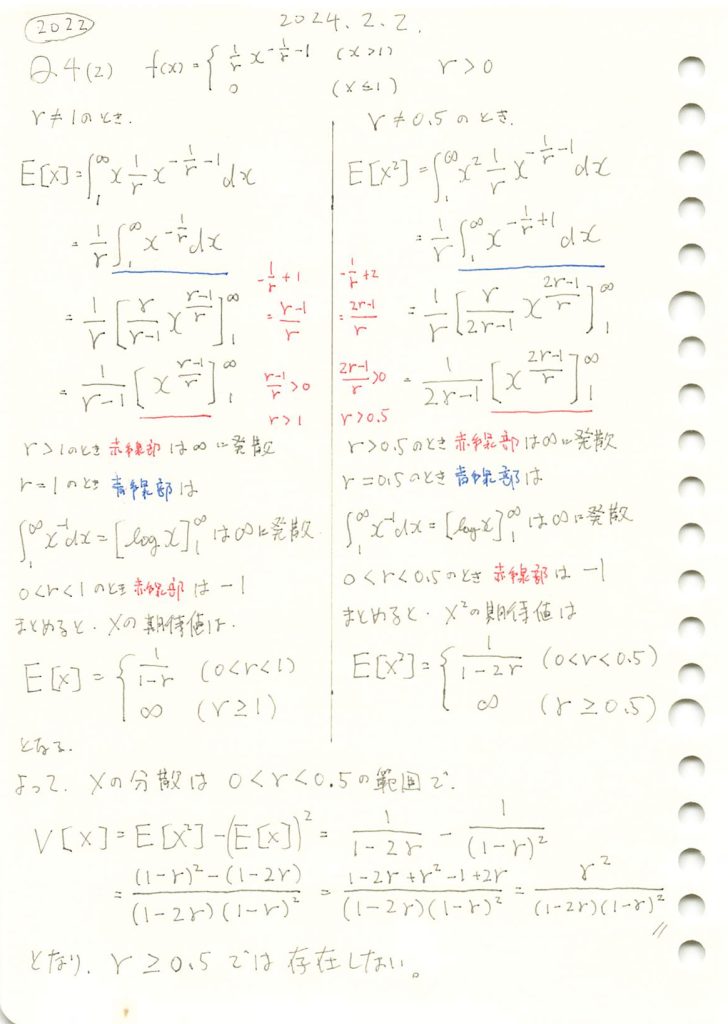
コード
数式を使った計算
# 2022 Q4(2) 2024.8.9
from sympy import init_printing
import sympy as sp
# これでTexの表示ができる
init_printing()
# シンボリック変数の定義
x, gamma = sp.symbols('x gamma', positive=True)
# 確率密度関数 f(x) の定義
f_x = (1/gamma) * x**(-(1/gamma + 1))
# 期待値 E[X] の計算
E_X = sp.integrate(x * f_x, (x, 1, sp.oo))
E_X_simplified = sp.simplify(E_X)
# E[X^2] の計算
E_X2 = sp.integrate(x**2 * f_x, (x, 1, sp.oo))
E_X2_simplified = sp.simplify(E_X2)
# 分散 V[X] の計算
V_X = E_X2_simplified - E_X_simplified**2
# 分散をさらに簡略化
V_X_simplified = sp.simplify(V_X)
V_X_factored = sp.factor(V_X_simplified)
# 結果を表示
E_X_simplified,E_X2_simplified,V_X_simplified,V_X_factored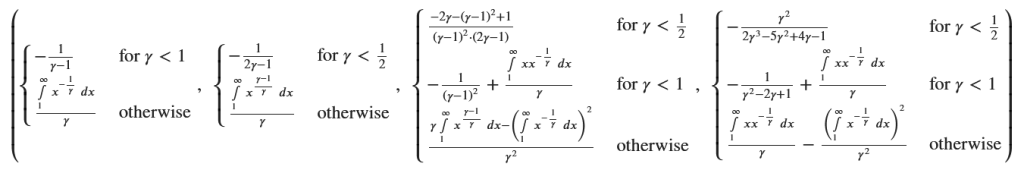
シミュレーションによる計算
# 2022 Q4(2) 2024.8.9
import numpy as np
import scipy.integrate as integrate
# パラメータの設定
gamma = 0.3 # 例として γ = 0.5 を設定
num_samples = 1000000 # サンプル数
# 確率密度関数 f(x) の定義
def pdf(x, gamma):
return (1/gamma) * x**(-(1/gamma + 1))
# 理論的な期待値 E[X] の計算
def theoretical_expected_value(gamma):
if gamma <= 0 or gamma >= 1:
return np.inf
else:
result, _ = integrate.quad(lambda x: x * pdf(x, gamma), 1, np.inf)
return result
# 理論的な分散 V[X] の計算
def theoretical_variance(gamma):
if gamma <= 0 or gamma >= 0.5:
return np.inf
else:
E_X = theoretical_expected_value(gamma)
E_X2, _ = integrate.quad(lambda x: x**2 * pdf(x, gamma), 1, np.inf)
return E_X2 - E_X**2
# シミュレーションによる確率変数 X のサンプリング
samples = (np.random.uniform(size=num_samples))**(-gamma)
# シミュレーションによる期待値 E[X] の推定
E_X_simulation = np.mean(samples)
# シミュレーションによる分散 V[X] の推定
V_X_simulation = np.var(samples)
# 理論値の計算
E_X_theoretical = theoretical_expected_value(gamma)
V_X_theoretical = theoretical_variance(gamma)
# 結果の表示
print(f"シミュレーションによる期待値 E[X]: {E_X_simulation}")
print(f"理論的な期待値 E[X]: {E_X_theoretical}")
print(f"シミュレーションによる分散 V[X]: {V_X_simulation}")
print(f"理論的な分散 V[X]: {V_X_theoretical}")
シミュレーションによる期待値 E[X]: 1.4284089260116615
理論的な期待値 E[X]: 1.4285714285714284
シミュレーションによる分散 V[X]: 0.4593987557711114
理論的な分散 V[X]: 0.45918367346938904