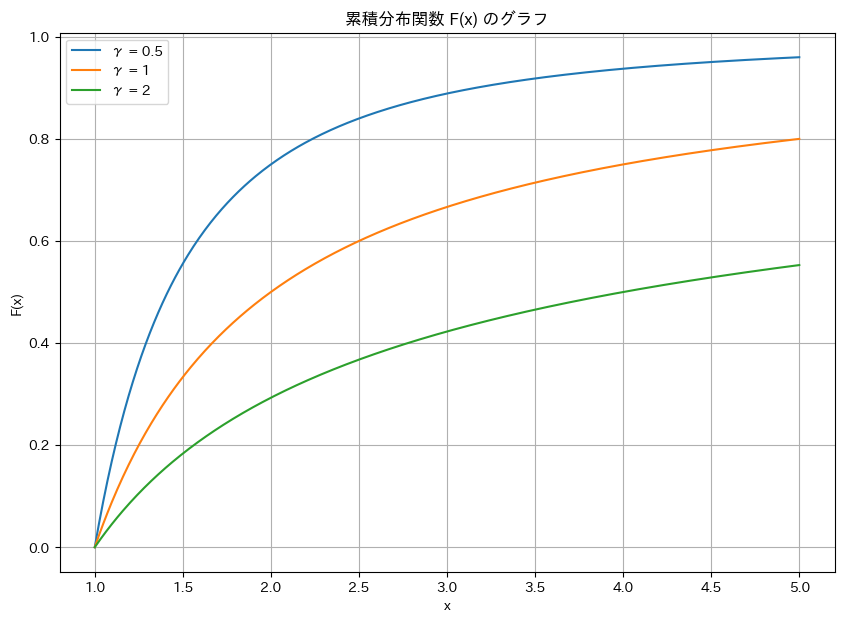
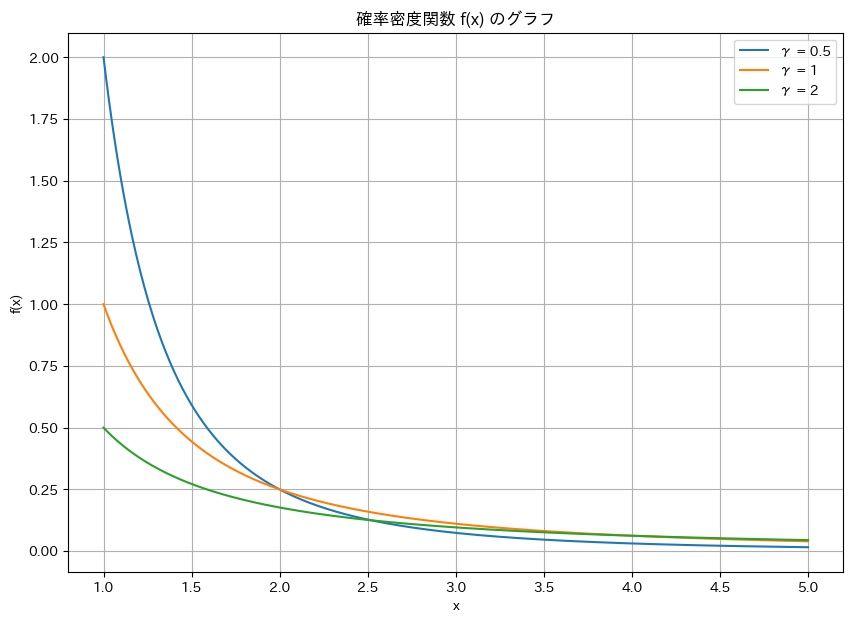
ある累積分布関数から確率密度関数を導いてグラフを描画しました。
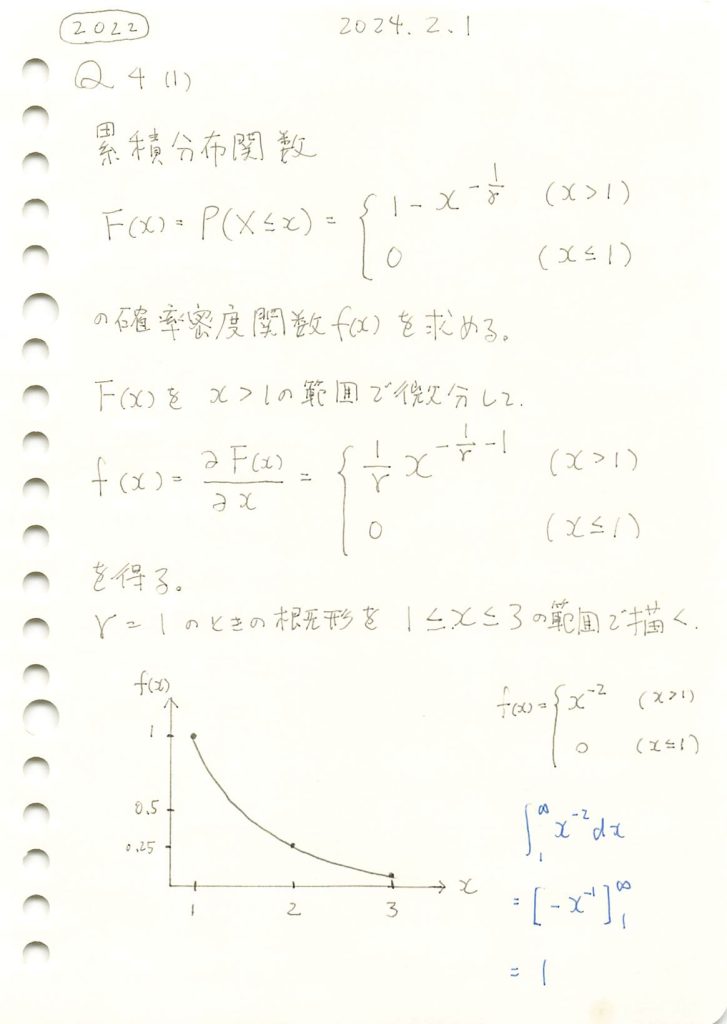
コード
確率密度関数 f(x) の描画
# 2022 Q4(1) 2024.8.8
import numpy as np
import matplotlib.pyplot as plt
def probability_density_function(x, gamma):
if x <= 1:
return 0
else:
return (1/gamma) * x**(-1/gamma-1)
# 配列のγ値に対するベクトル化された関数
def f_array(x, gammas):
y_values = np.zeros((len(gammas), len(x)))
for i, gamma in enumerate(gammas):
y_values[i] = [probability_density_function(xi, gamma) for xi in x]
return y_values
x_values = np.linspace(1.00001, 5, 500)
gammas = [0.5, 1, 2]
y_values_pdf_array = f_array(x_values, gammas)
plt.figure(figsize=(10, 7))
for i, gamma in enumerate(gammas):
plt.plot(x_values, y_values_pdf_array[i], label=f"γ = {gamma}")
plt.title("確率密度関数 f(x) のグラフ")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.grid(True)
plt.legend()
plt.show()
累積分布関数 F(x) の描画
# 2022 Q4(1) 2024.8.8
import numpy as np
import matplotlib.pyplot as plt
# 累積分布関数を定義
def F(x, gamma):
if x <= 1:
return 0
else:
return 1 - x**(-1/gamma)
# 配列のγ値に対するベクトル化された関数
def F_array(x, gammas):
y_values = np.zeros((len(gammas), len(x)))
for i, gamma in enumerate(gammas):
y_values[i] = [F(xi, gamma) for xi in x]
return y_values
x_values = np.linspace(1, 5, 500)
gammas = [0.5, 1, 2]
y_values_array = F_array(x_values, gammas)
plt.figure(figsize=(10, 7))
for i, gamma in enumerate(gammas):
plt.plot(x_values, y_values_array[i], label=f"γ = {gamma}")
plt.title("累積分布関数 F(x) のグラフ")
plt.xlabel("x")
plt.ylabel("F(x)")
plt.grid(True)
plt.legend()
plt.show()