標本平均とP値の関係をグラフで描きました。

コード
n=10のときの標本平均![]() とP値の関係をグラフで示します。また
とP値の関係をグラフで示します。また![]() のP値を計算します。
のP値を計算します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 問題の設定
n = 10 # サンプルサイズ
mu_0 = 0 # 帰無仮説の平均
sigma = 1 # 分散1なので標準偏差は1
alpha = 0.05 # 有意水準
critical_value = norm.ppf(1 - alpha) # 上側確率100α%点
threshold = critical_value / np.sqrt(n) # 棄却域の閾値
# 標本平均の値
x_bar_values = np.linspace(0, 1, 100) # 標本平均の範囲
p_values = 1 - norm.cdf((x_bar_values - mu_0) * np.sqrt(n)) # P値を計算
# 指定された x̄ = 0.3, 0.6 の場合の P値
x_bar_special = [0.3, 0.6]
p_values_special = 1 - norm.cdf((np.array(x_bar_special) - mu_0) * np.sqrt(n))
# 結果出力
print("指定された標本平均 x̄ に対応する P値:")
for x, p in zip(x_bar_special, p_values_special):
print(f" 標本平均 x̄ = {x:.1f} の場合の P値: {p:.3f}")
# グラフの描画
plt.figure(figsize=(8, 5))
plt.plot(x_bar_values, p_values, label="P値の挙動", color="orange")
plt.axhline(y=alpha, color="red", linestyle="--", label=f"有意水準 α={alpha}")
plt.scatter(x_bar_special, p_values_special, color="blue", label="指定点 (0.3, 0.6)")
for x, p in zip(x_bar_special, p_values_special):
plt.text(x, p, f"({x:.1f}, {p:.3f})", fontsize=10, color="blue")
plt.xlabel("標本平均 $\\bar{x}$", fontsize=12)
plt.ylabel("P値", fontsize=12)
plt.title("P値の挙動 (標本平均 $\\bar{x}$ の範囲)", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()指定された標本平均 x̄ に対応する P値:
標本平均 x̄ = 0.3 の場合の P値: 0.171
標本平均 x̄ = 0.6 の場合の P値: 0.029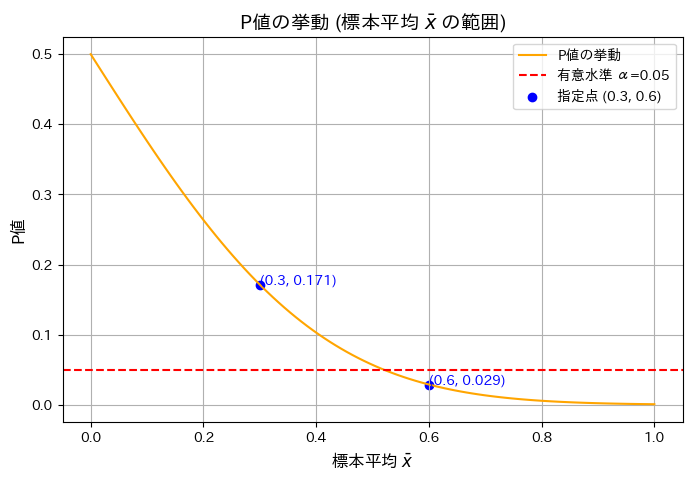
グラフの概形が描けました。標本平均![]() が大きくなるにつれてP値が減少することを確認しました。
が大きくなるにつれてP値が減少することを確認しました。