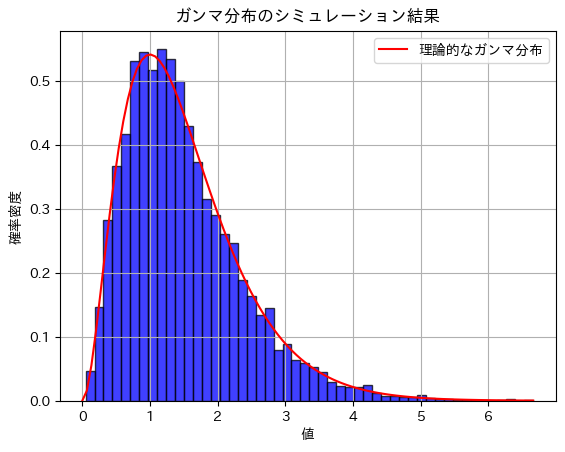
ガンマ分布の期待値と分散を求めました。
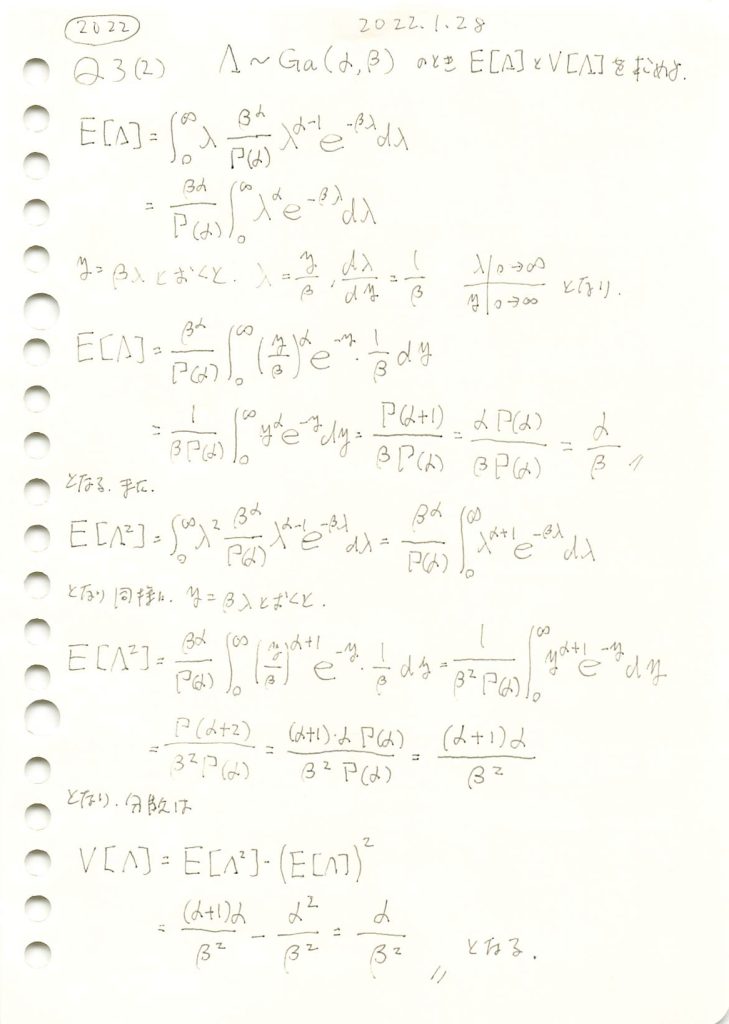
コード
数式を使った計算
## 2022 Q3(2) 2024.8.4
import sympy as sp
# 定義
lambda_var = sp.symbols('lambda')
alpha, beta = sp.symbols('alpha beta', positive=True)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha-1) * sp.exp(-beta * lambda_var)
# 期待値 E[Λ] の計算
expected_value = sp.integrate(lambda_var * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# E[Λ^2] の計算
expected_value_Lambda2 = sp.integrate(lambda_var**2 * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# 分散 V[Λ] の計算
variance = (expected_value_Lambda2 - expected_value**2).simplify()
# 結果を辞書形式で表示
{
"期待値 E[Λ]": expected_value,
"分散 V[Λ]": variance
}{'期待値 E[Λ]': alpha/beta, '分散 V[Λ]': alpha/beta**2}シミュレーションによる計算
## 2022 Q3(2) 2024.8.4
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# サンプルサイズ
sample_size = 10000
# ガンマ分布に従う乱数を生成
samples = np.random.gamma(alpha, 1/beta, sample_size)
# 期待値と分散の計算
expected_value = np.mean(samples)
variance = np.var(samples)
# 結果の表示
print(f"期待値のシミュレーション結果: {expected_value}")
print(f"分散のシミュレーション結果: {variance}")
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なガンマ分布の確率密度関数をプロット
x = np.linspace(0, max(samples), 100)
gamma_pdf = gamma.pdf(x, alpha, scale=1/beta)
plt.plot(x, gamma_pdf, 'r', linestyle='-', label='理論的なガンマ分布')
# グラフのタイトルとラベル
plt.title('ガンマ分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()期待値のシミュレーション結果: 1.4947527551017439
分散のシミュレーション結果: 0.7452822182213243# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# 理論値の計算
theoretical_expected_value = alpha / beta
theoretical_variance = alpha / beta**2
# 結果の表示
print(f"理論値 - 期待値: {theoretical_expected_value}")
print(f"理論値 - 分散: {theoretical_variance}")理論値 - 期待値: 1.5
理論値 - 分散: 0.75