ホーム » コードあり » 2022 Q2(5)

2022 Q2(5)

投稿者: in コードあり, 統計検定1級 2022年 統計数理 投稿日: 最終更新日:

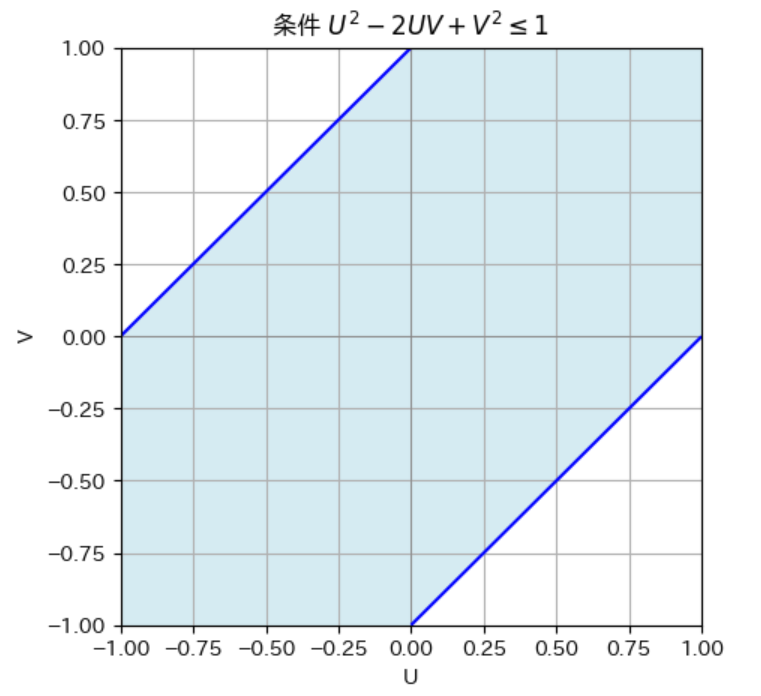
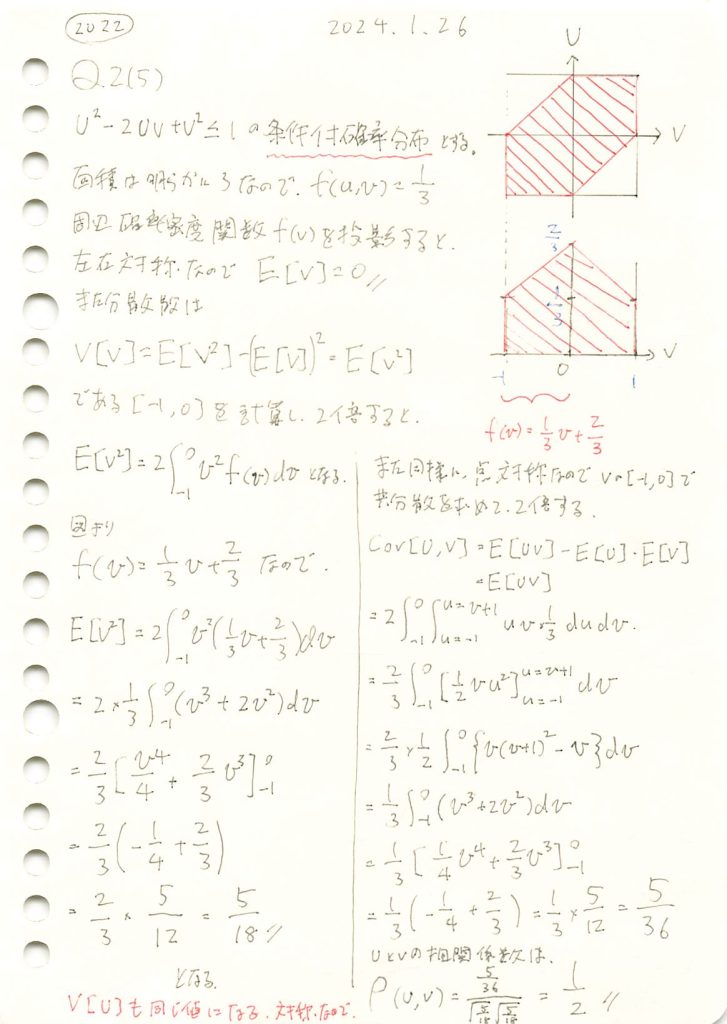
2変数の条件付き確率を表す図形から相関係数を求める問題をやりました。

コード

二重積分による計算

# 2022 Q2(5)  2024.8.2

import numpy as np
from scipy.integrate import dblquad

# 確率密度関数
def pdf(u, v):
    return 1/3 if (u**2 - 2*u*v + v**2 <= 1) else 0

# 期待値 E[U] を計算
E_U, _ = dblquad(lambda v, u: u * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)
# 期待値 E[V] を計算
E_V, _ = dblquad(lambda v, u: v * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)

# 期待値 E[U^2] を計算
E_U2, _ = dblquad(lambda v, u: u**2 * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)
# 期待値 E[V^2] を計算
E_V2, _ = dblquad(lambda v, u: v**2 * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)

# 分散 Var(U) を計算
Var_U = E_U2 - E_U**2
# 分散 Var(V) を計算
Var_V = E_V2 - E_V**2

# 共分散 Cov(U, V) を計算
Cov_UV, _ = dblquad(lambda v, u: u*v * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)

# 相関係数 ρ(U, V) を計算
rho_UV = Cov_UV / np.sqrt(Var_U * Var_V)

E_U, E_V, Var_U, Var_V, rho_UV

(0.0, 0.0, 0.27777777931630593, 0.2777565638412289, 0.5000186020617616)

モンテカルロ法による計算

# 2022 Q2(5)  2024.8.2

import numpy as np

# モンテカルロ法の設定
num_points = 10000

# UとVの一様乱数を生成
U = np.random.uniform(-1, 1, num_points)
V = np.random.uniform(-1, 1, num_points)

# 条件 U^2 - 2UV + V^2 <= 1 を満たす点をフィルタリング
condition = U**2 - 2*U*V + V**2 <= 1
U_filtered = U[condition]
V_filtered = V[condition]

# フィルタリングされた点数
num_filtered_points = len(U_filtered)

# 期待値 E[U] と E[V] の計算
E_U = np.mean(U_filtered)
E_V = np.mean(V_filtered)

# 分散 Var(U) と Var(V) の計算
Var_U = np.var(U_filtered, ddof=1)
Var_V = np.var(V_filtered, ddof=1)

# 共分散 Cov(U, V) の計算
Cov_UV = np.cov(U_filtered, V_filtered, ddof=1)[0, 1]

# 相関係数 ρ(U, V) の計算
rho_UV = Cov_UV / np.sqrt(Var_U * Var_V)

E_U, E_V, Var_U, Var_V, rho_UV, num_filtered_points

(-0.0030089627151707833,
 -0.0028658643404494717,
 0.2780688116636205,
 0.2779098545694732,
 0.4835460989080292,
 7488)

アルゴリズム

モンテカルロ法

  1. 初期設定
    • シミュレーションで使用する点の数を設定する。
  2. 乱数の生成
    • 範囲 [−1,1] でランダムに U と V の値を生成する。
  3. 条件の適用
    • 生成した点の中で、条件 [ U^2 - 2UV + V^2 \leq 1 ] を満たす点を選び出す。
  4. 期待値の計算
    • 条件を満たした点の U と V の平均値を計算する。
  5. 分散の計算
    • 条件を満たした点の U と V の分散を計算する。
  6. 相関係数の計算
    • 条件を満たした点の U と V の共分散を計算し、それを用いて相関係数を求める。
  7. 結果の表示
    • 計算した期待値、分散、相関係数、および条件を満たした点の数を表示する。

プロット