特異値分解を用いてMが行フルランクでない場合に先の問の条件を満たすAが存在するか論ずる問題をやりました。

コード
M行列のrank(M)を5~1に変化させて、A行列を特異値分解により計算し、![]() の変化を確認します。
の変化を確認します。
# 2021 Q5(4) 2024.9.8
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# l, n を定義
l = 5 # Lの行数
n = 5 # LとMの列数 (xの次元)
# 再現性のために乱数のシードを固定
np.random.seed(43)
# L行列を生成。-10から10の間の整数でランダムなL行列
L = np.random.randint(-10, 11, size=(l, n))
# N(0, 1) に従う乱数ベクトル x を生成 (サンプル数を1000000に設定)
sample_size = 1000000
x = np.random.randn(n, sample_size)
# グラフの準備(2行3列のグリッドに5つのヒートマップを描画するので、6個目は空白にする)
fig, axs = plt.subplots(2, 3, figsize=(15, 10)) # 2行3列のサブプロットを作成
axs = axs.flatten() # インデックス操作を簡単にするためフラット化
# m を 5 から 1 まで変化させて実験
for idx, m in enumerate(range(5, 0, -1)):
# M行列を生成。-10から10の間の整数でランダムなM行列
while True:
M = np.random.randint(-10, 11, size=(m, n))
if np.linalg.matrix_rank(M) == m: # Mが行フルランクかどうかを判定
break
# Mの特異値分解: M = U * D * V^T
U, D, VT = np.linalg.svd(M)
# 特異値の逆数を作成 (ゼロ除算を回避)
D_inv = np.diag([1/d if d > 1e-10 else 0 for d in D]) # Dの逆行列。特異値が0のところは無視
# L の形状に応じて A を計算
A = np.dot(np.dot(np.dot(L, VT.T[:n, :m]), D_inv[:m, :m]), U.T[:m, :])
# Lx, Mx, AMx を計算
Lx = np.dot(L, x) # lxサンプル数の行列
Mx = np.dot(M, x) # mxサンプル数の行列
AMx = np.dot(A, Mx) # AMx の計算
# 共分散行列 Cov(Lx - AMx, Mx) を計算
cov_matrix_Lx_AMx_Mx = np.zeros((l, m))
for i in range(l):
for j in range(m):
cov_matrix_Lx_AMx_Mx[i, j] = np.cov(Lx[i, :] - AMx[i, :], Mx[j, :])[0, 1]
# 各サブプロットにヒートマップを描画
sns.heatmap(cov_matrix_Lx_AMx_Mx, cmap="coolwarm", annot=True, fmt=".2f", center=0, vmin=-1, vmax=1, ax=axs[idx])
axs[idx].set_title(f'm={m}')
# 6個目のサブプロットを消す(最後の空のプロットを非表示にする)
fig.delaxes(axs[5])
# グラフを描画
plt.suptitle('共分散行列 Cov(Lx - AMx, Mx) の変化 (mの変化)', fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.96]) # タイトルとレイアウト調整
plt.show()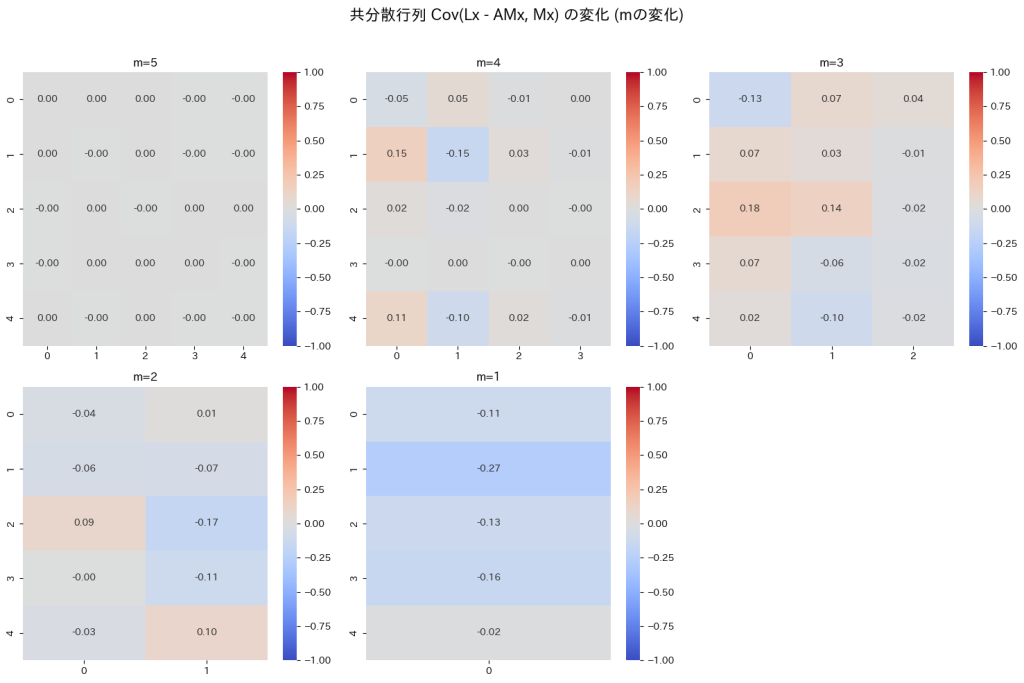
m=1~5のどのランクにおいても、A行列が見つかり![]() はゼロ行列に近づきました。またmが減少するにつれて
はゼロ行列に近づきました。またmが減少するにつれて![]() は大きくなることを確認しました。
は大きくなることを確認しました。