二つの式を互いに独立にする、実行列Aを求める問題をやりました。

コード
A行列を用いて、Lx – AMx と Mx の独立性を検証してみます。
まず、L行列とM行列を乱数で生成します。ただしM行列は行フルランクになるようします。
![]() も求めます。
も求めます。
# 2021 Q5(3) 2024.9.7
import numpy as np
# l, m, n を定義
l = 5 # Lの行数
m = 5 # Mの行数
n = 5 # LとMの列数 (xの次元)
# 再現性のために乱数のシードを固定
np.random.seed(43)
# L行列を生成。-10から10の間の整数でランダムなL行列
L = np.random.randint(-10, 11, size=(l, n))
# M行列を生成。-10から10の間の整数でランダムなM行列
# 但し、M がフルランク(ランクが n と等しい)になるまで繰り返す
while True:
M = np.random.randint(-10, 11, size=(m, n))
if np.linalg.matrix_rank(M) == m: # Mが行フルランクかどうかを判定
break
# A行列を求める: A = L * M^T * (M * M^T)^(-1)
A = np.dot(np.dot(L, M.T), np.linalg.inv(np.dot(M, M.T)))
# 結果を表示
print("L行列:\n", L)
print("\nM行列:\n", M)
print("\nA行列 (L, Mから計算):\n", A)L行列:
[[ -6 -10 7 6 9]
[ 7 -8 4 -10 -7]
[ 8 1 -9 5 -8]
[ 1 -8 -7 -6 -6]
[ 6 2 5 -10 0]]
M行列:
[[ 6 -1 -8 6 10]
[ -6 -1 -3 10 5]
[ -2 -10 -7 -8 -1]
[ 1 6 -2 0 -3]
[ -7 9 -8 4 0]]
A行列 (L, Mから計算):
[[-0.11382722 0.14885099 -0.47741032 -2.97220233 0.34379272]
[-0.2300306 0.14696309 0.62486166 1.60321594 -1.2726385 ]
[ 0.0655719 2.52963674 1.25657509 6.68244255 -2.65929952]
[-0.16838096 0.98942126 1.29721372 2.65536098 -1.12655426]
[ 0.26046481 -1.95599245 -0.55640909 -2.20630167 0.88646572]]次に、![]() がゼロ行列になっているか確認します
がゼロ行列になっているか確認します
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# N(0, 1) に従う乱数ベクトル x を生成 (サンプル数を1000000に設定)
sample_size = 1000000
x = np.random.randn(n, sample_size)
# Lx, Mx, AMx を計算
Lx = np.dot(L, x) # lxサンプル数の行列
Mx = np.dot(M, x) # mxサンプル数の行列
AMx = np.dot(A, Mx) # AMx の計算
# 共分散行列 Cov(Lx - AMx, Mx) を計算
cov_matrix_Lx_AMx_Mx = np.zeros((l, m))
for i in range(l):
for j in range(m):
cov_matrix_Lx_AMx_Mx[i, j] = np.cov(Lx[i, :] - AMx[i, :], Mx[j, :])[0, 1]
# ヒートマップを描画
plt.figure(figsize=(6, 6))
# 共分散行列 Cov(Lx - AMx, Mx) のヒートマップ
sns.heatmap(cov_matrix_Lx_AMx_Mx, cmap="coolwarm", annot=True, fmt=".2f", center=0, vmin=-1, vmax=1)
plt.title('共分散行列 Cov(Lx - AMx, Mx)')
plt.tight_layout()
plt.show()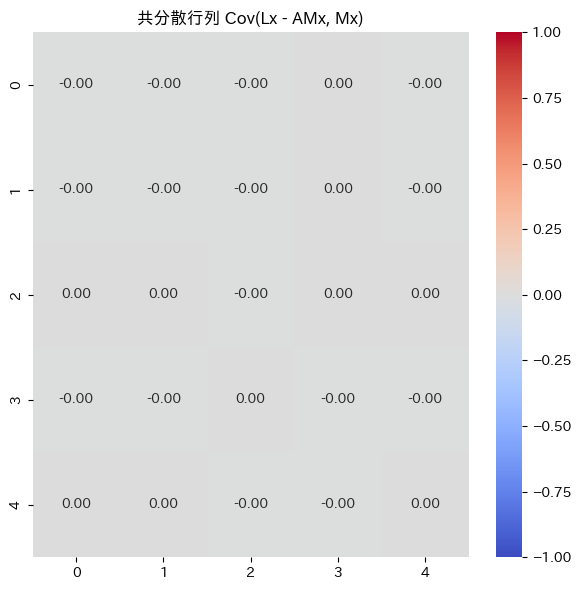
ゼロ行列になっています。検証ができました。