線形変換により得られた二つのベクトルが独立となる条件を求める問題をやりました。

コード
各行ベクトルが直交している行列LとMを生成します
# 2021 Q5(2) 2024.9.6
import numpy as np
# 乱数で4つの要素を持つ基準ベクトルを生成 (整数で0以外の値のみ)
def generate_random_integer_vector_4(n=4):
return np.random.randint(1, 10, size=n) # 1から9の範囲で整数を生成
# 生成した基準ベクトルを使って、並行するベクトルを生成
def generate_parallel_matrix_4(v, scale_factors):
L = np.array([scale * v for scale in scale_factors])
return L
# ベクトル v に直交するベクトルを生成する関数
# グラム・シュミット法を適用して、基準ベクトルに直交するベクトルを作る
def generate_orthogonal_vectors_4(v):
orthogonal_vectors = []
for _ in range(5):
candidate = np.random.randint(1, 10, size=v.shape) # 新たな候補ベクトル
# 直交条件:v と candidate の内積が 0 になるように調整
adjustment = np.dot(candidate, v) / np.dot(v, v)
orthogonal_vector = candidate - adjustment * v # 直交ベクトルにする
orthogonal_vectors.append(orthogonal_vector)
return np.array(orthogonal_vectors)
# 基準ベクトルを生成
v_base = generate_random_integer_vector_4()
# 基準ベクトルと並行するベクトルを5つ作る
scale_factors_5 = [1, 2, 3, 4, 5]
L_5x4 = generate_parallel_matrix_4(v_base, scale_factors_5)
# 基準ベクトルに直交するベクトルを5つ作る
M_5x4 = generate_orthogonal_vectors_4(v_base)
# 行列 L, M の表示とその積の確認
L_5x4, M_5x4, np.dot(L_5x4, M_5x4.T) # L, M, そしてその積を表示(array([[ 7, 1, 6, 8],
[14, 2, 12, 16],
[21, 3, 18, 24],
[28, 4, 24, 32],
[35, 5, 30, 40]]),
array([[-3.01333333, 8.42666667, -2.44 , 3.41333333],
[-1.68666667, 6.47333333, 3.84 , -2.21333333],
[ 1.28666667, 4.32666667, 0.96 , -2.38666667],
[ 1.14666667, 3.30666667, 2.84 , -3.54666667],
[-2.73333333, 4.46666667, -1.2 , 2.73333333]]),
array([[-7.10542736e-15, 7.10542736e-15, 0.00000000e+00,
-3.55271368e-15, 0.00000000e+00],
[-1.42108547e-14, 1.42108547e-14, 0.00000000e+00,
-7.10542736e-15, 0.00000000e+00],
[-2.13162821e-14, 2.13162821e-14, 7.10542736e-15,
0.00000000e+00, -7.10542736e-15],
[-2.84217094e-14, 2.84217094e-14, 0.00000000e+00,
-1.42108547e-14, 0.00000000e+00],
[-3.55271368e-14, 2.84217094e-14, 0.00000000e+00,
-2.84217094e-14, -7.10542736e-15]]))行列LとMを生成し、![]() を求めました。
を求めました。![]() はほぼゼロ行列になっています。
はほぼゼロ行列になっています。
LxとMxの共分散行列を求めます
# 2021 Q5(2) 2024.9.6
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# l, m, n を定義
l = 5 # Lの行数
m = 5 # Mの行数
n = 4 # LとMの列数 (xの次元)
# L と M を定義 (与えられた行列を使用)
L = np.array([[7, 1, 6, 8],
[14, 2, 12, 16],
[21, 3, 18, 24],
[28, 4, 24, 32],
[35, 5, 30, 40]])
M = np.array([[-3.01333333, 8.42666667, -2.44, 3.41333333],
[-1.68666667, 6.47333333, 3.84, -2.21333333],
[1.28666667, 4.32666667, 0.96, -2.38666667],
[1.14666667, 3.30666667, 2.84, -3.54666667],
[-2.73333333, 4.46666667, -1.2, 2.73333333]])
# N(0, 1) に従う乱数ベクトル x を生成 (サンプル数を10000000にする)
sample_size = 10000000
x = np.random.randn(n, sample_size)
# Lx と Mx を計算
Lx = np.dot(L, x) # lxサンプル数の行列
Mx = np.dot(M, x) # mxサンプル数の行列
# 共分散行列 Cov(Lx, Mx) を計算
cov_matrix = np.zeros((l, m))
for i in range(l):
for j in range(m):
cov_matrix[i, j] = np.cov(Lx[i, :], Mx[j, :])[0, 1]
# L * M^T の積を再計算
LM_T = np.dot(L, M.T)
# ヒートマップを描画
plt.figure(figsize=(12, 6))
# 共分散行列のヒートマップ
plt.subplot(1, 2, 1)
sns.heatmap(cov_matrix, cmap="coolwarm", annot=True, fmt=".2f", center=0, vmin=-1, vmax=1)
plt.title(f'共分散行列 Cov(Lx, Mx)')
# L * M^T のヒートマップ
plt.subplot(1, 2, 2)
sns.heatmap(LM_T, cmap="coolwarm", annot=True, fmt=".2f", center=0, vmin=-1, vmax=1)
plt.title(f'行列 L * M^T')
plt.tight_layout()
plt.show()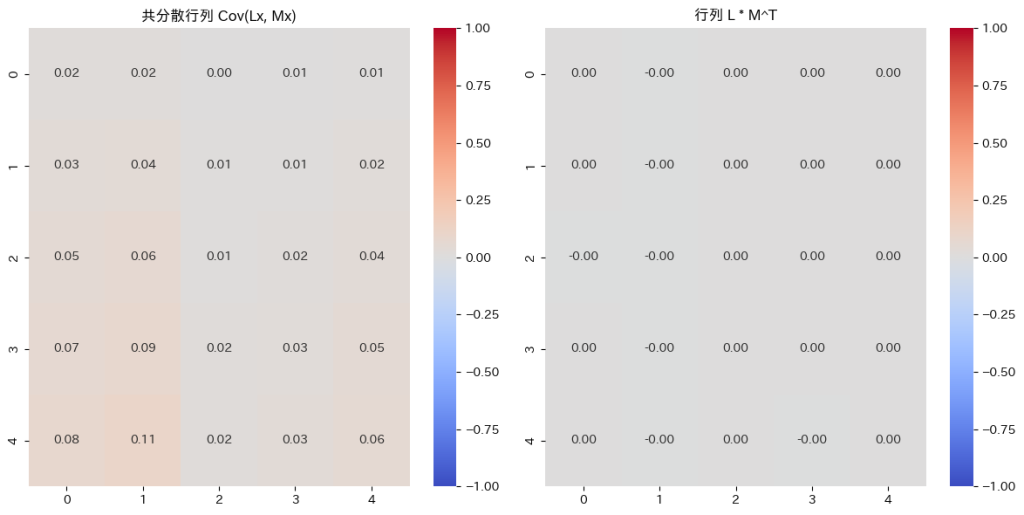
Cov(Lx,Mx)はゼロ行列に近づきます。その必要十分条件は![]() がゼロ行列になることです。
がゼロ行列になることです。
ここで注意が必要なのは、LxとMxは確率変数から成るベクトルであり、Cov(Lx,Mx)はLxとMxのそれぞれの確率変数同士の共分散を計算し、それを行列としてまとめたものです。