確率変数と母平均の差に関する期待値の計算をしました。
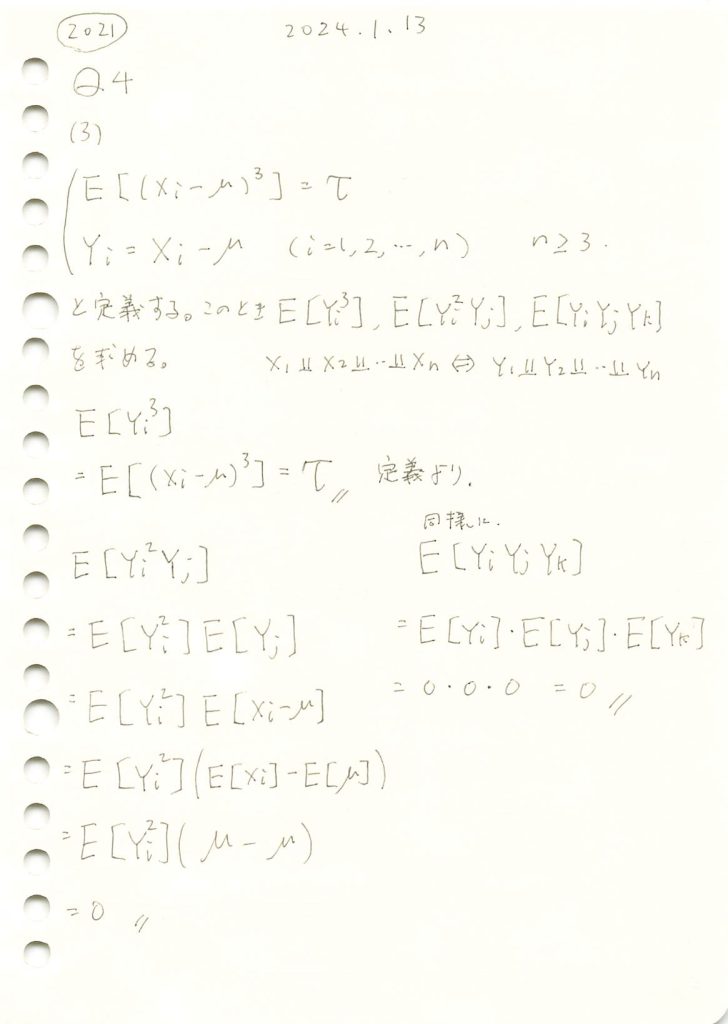
コード
Xiが正規分布(μ=0, σ=1)に従う場合
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 1000 # サンプル数
mu, sigma = 0, 1 # 正規分布の平均と標準偏差
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
Y_i_cubed_values = []
Y_i_squared_Y_j_values = []
Y_i_Y_j_Y_k_values = []
# シミュレーションを実行
for _ in range(iterations):
X_i = np.random.normal(mu, sigma, size=n)
X_j = np.random.normal(mu, sigma, size=n)
X_k = np.random.normal(mu, sigma, size=n)
Y_i = X_i - mu
Y_j = X_j - mu
Y_k = X_k - mu
Y_i_cubed_values.append(np.mean(Y_i**3))
Y_i_squared_Y_j_values.append(np.mean(Y_i**2 * Y_j))
Y_i_Y_j_Y_k_values.append(np.mean(Y_i * Y_j * Y_k))
# グラフを横に並べて表示
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# (1) E[Y_i^3] の分布
axes[0].hist(Y_i_cubed_values, bins=50, alpha=0.75)
axes[0].axvline(np.mean(Y_i_cubed_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[0].set_title(r"正規分布における $E[Y_i^3]$ の分布")
axes[0].set_xlabel('値')
axes[0].set_ylabel('頻度')
axes[0].legend()
# (2) E[Y_i^2 Y_j] の分布
axes[1].hist(Y_i_squared_Y_j_values, bins=50, alpha=0.75)
axes[1].axvline(np.mean(Y_i_squared_Y_j_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[1].set_title(r"正規分布における $E[Y_i^2 Y_j]$ の分布")
axes[1].set_xlabel('値')
axes[1].set_ylabel('頻度')
axes[1].legend()
# (3) E[Y_i Y_j Y_k] の分布
axes[2].hist(Y_i_Y_j_Y_k_values, bins=50, alpha=0.75)
axes[2].axvline(np.mean(Y_i_Y_j_Y_k_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[2].set_title(r"正規分布における $E[Y_i Y_j Y_k]$ の分布")
axes[2].set_xlabel('値')
axes[2].set_ylabel('頻度')
axes[2].legend()
# グラフを表示
plt.tight_layout()
plt.show()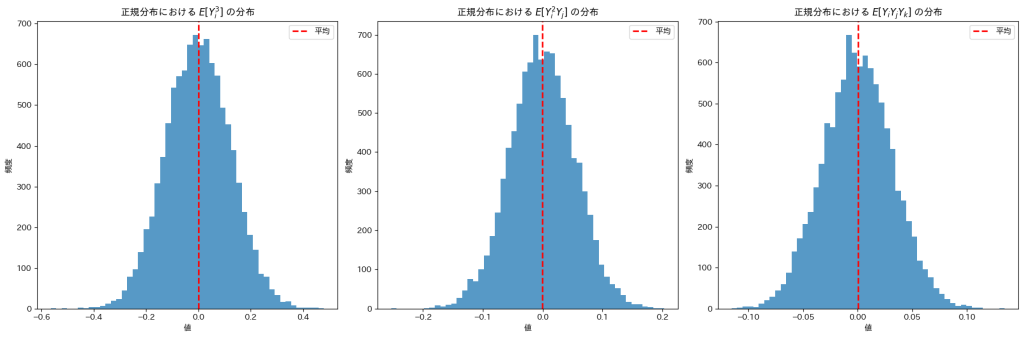
![]() は0になります
は0になります
Xiが指数分布(λ=1)に従う場合
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 1000 # サンプル数
scale = 1.0 # 指数分布のスケールパラメータ(1/λ)
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
Y_i_cubed_values = []
Y_i_squared_Y_j_values = []
Y_i_Y_j_Y_k_values = []
# シミュレーションを実行
for _ in range(iterations):
X_i = np.random.exponential(scale=scale, size=n)
X_j = np.random.exponential(scale=scale, size=n)
X_k = np.random.exponential(scale=scale, size=n)
Y_i = X_i - np.mean(X_i)
Y_j = X_j - np.mean(X_j)
Y_k = X_k - np.mean(X_k)
Y_i_cubed_values.append(np.mean(Y_i**3))
Y_i_squared_Y_j_values.append(np.mean(Y_i**2 * Y_j))
Y_i_Y_j_Y_k_values.append(np.mean(Y_i * Y_j * Y_k))
# グラフを横に並べて表示
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# (1) E[Y_i^3] の分布
axes[0].hist(Y_i_cubed_values, bins=50, alpha=0.75)
axes[0].axvline(np.mean(Y_i_cubed_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[0].set_title(r"指数分布における $E[Y_i^3]$ の分布")
axes[0].set_xlabel('値')
axes[0].set_ylabel('頻度')
axes[0].legend()
# (2) E[Y_i^2 Y_j] の分布
axes[1].hist(Y_i_squared_Y_j_values, bins=50, alpha=0.75)
axes[1].axvline(np.mean(Y_i_squared_Y_j_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[1].set_title(r"指数分布における $E[Y_i^2 Y_j]$ の分布")
axes[1].set_xlabel('値')
axes[1].set_ylabel('頻度')
axes[1].legend()
# (3) E[Y_i Y_j Y_k] の分布
axes[2].hist(Y_i_Y_j_Y_k_values, bins=50, alpha=0.75)
axes[2].axvline(np.mean(Y_i_Y_j_Y_k_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[2].set_title(r"指数分布における $E[Y_i Y_j Y_k]$ の分布")
axes[2].set_xlabel('値')
axes[2].set_ylabel('頻度')
axes[2].legend()
# グラフを表示
plt.tight_layout()
plt.show()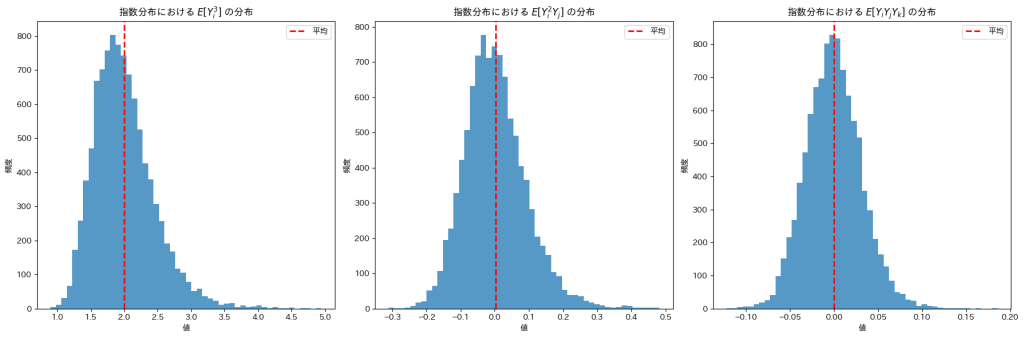
![]() は0になりますが、
は0になりますが、![]() は2付近の値をとっているようです。
は2付近の値をとっているようです。
Xiがガンマ分布(形状パラメータ=2, スケールパラメータ=2)に従う場合
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 1000 # サンプル数
shape, scale = 2.0, 2.0 # ガンマ分布の形状パラメータとスケールパラメータ
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
Y_i_cubed_values = []
Y_i_squared_Y_j_values = []
Y_i_Y_j_Y_k_values = []
# シミュレーションを実行
for _ in range(iterations):
X_i = np.random.gamma(shape, scale, size=n)
X_j = np.random.gamma(shape, scale, size=n)
X_k = np.random.gamma(shape, scale, size=n)
Y_i = X_i - np.mean(X_i)
Y_j = X_j - np.mean(X_j)
Y_k = X_k - np.mean(X_k)
Y_i_cubed_values.append(np.mean(Y_i**3))
Y_i_squared_Y_j_values.append(np.mean(Y_i**2 * Y_j))
Y_i_Y_j_Y_k_values.append(np.mean(Y_i * Y_j * Y_k))
# グラフを横に並べて表示
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# (1) E[Y_i^3] の分布
axes[0].hist(Y_i_cubed_values, bins=50, alpha=0.75)
axes[0].axvline(np.mean(Y_i_cubed_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[0].set_title(r"ガンマ分布における $E[Y_i^3]$ の分布")
axes[0].set_xlabel('値')
axes[0].set_ylabel('頻度')
axes[0].legend()
# (2) E[Y_i^2 Y_j] の分布
axes[1].hist(Y_i_squared_Y_j_values, bins=50, alpha=0.75)
axes[1].axvline(np.mean(Y_i_squared_Y_j_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[1].set_title(r"ガンマ分布における $E[Y_i^2 Y_j]$ の分布")
axes[1].set_xlabel('値')
axes[1].set_ylabel('頻度')
axes[1].legend()
# (3) E[Y_i Y_j Y_k] の分布
axes[2].hist(Y_i_Y_j_Y_k_values, bins=50, alpha=0.75)
axes[2].axvline(np.mean(Y_i_Y_j_Y_k_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[2].set_title(r"ガンマ分布における $E[Y_i Y_j Y_k]$ の分布")
axes[2].set_xlabel('値')
axes[2].set_ylabel('頻度')
axes[2].legend()
# グラフを表示
plt.tight_layout()
plt.show()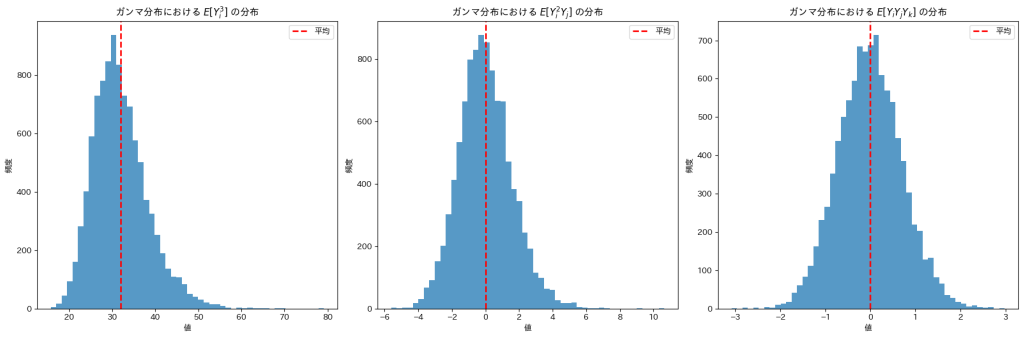
![]() は0になりますが、
は0になりますが、![]() は32付近の値をとっているようです。
は32付近の値をとっているようです。