平均の分散と、同じ分布に従う2変数の差の3乗の期待値を求めました。

(1)標本平均の分散
# 2021 Q4(1) 2024.8.31
import numpy as np
# パラメータの設定
n = 100 # サンプル数
mu = 0 # 平均
sigma = 1 # 標準偏差
iterations = 10000 # シミュレーション回数
# 各シミュレーションで得た標本平均を格納するリスト
sample_means = []
for _ in range(iterations):
# 正規分布に従う乱数を生成
X = np.random.normal(loc=mu, scale=sigma, size=n)
# 標本平均を計算
X_bar = np.mean(X)
sample_means.append(X_bar)
# 標本平均の分散を計算
estimated_variance_of_sample_mean = np.var(sample_means)
# 理論的な分散
theoretical_variance = sigma**2 / n
print(f"理論的な分散: {theoretical_variance}")
print(f"推定された標本平均の分散: {estimated_variance_of_sample_mean}")
理論的な分散: 0.01
推定された標本平均の分散: 0.009838287336429174分布を見てみます
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 100 # サンプル数
mu = 0 # 平均
sigma = 1 # 標準偏差
iterations = 10000 # シミュレーション回数
# 分散の推定値を格納するリスト
estimated_variances = []
for _ in range(iterations):
# 正規分布に従う乱数を生成
X = np.random.normal(loc=mu, scale=sigma, size=n)
# 標本平均の分散を計算
estimated_variance = np.var(X) / n
estimated_variances.append(estimated_variance)
# 理論的な分散
theoretical_variance = sigma**2 / n
# 視覚化
plt.figure(figsize=(10, 6))
plt.hist(estimated_variances, bins=100, alpha=0.75, label='推定された分散', range=(0.005, 0.015))
plt.axvline(theoretical_variance, color='red', linestyle='dashed', linewidth=2, label=f'理論的な分散 = {theoretical_variance}')
plt.xlabel('分散')
plt.ylabel('頻度')
plt.title(f'{iterations}回のシミュレーションにおける推定された分散の分布\n(サンプルサイズ = {n})')
plt.legend()
plt.grid(True)
plt.show()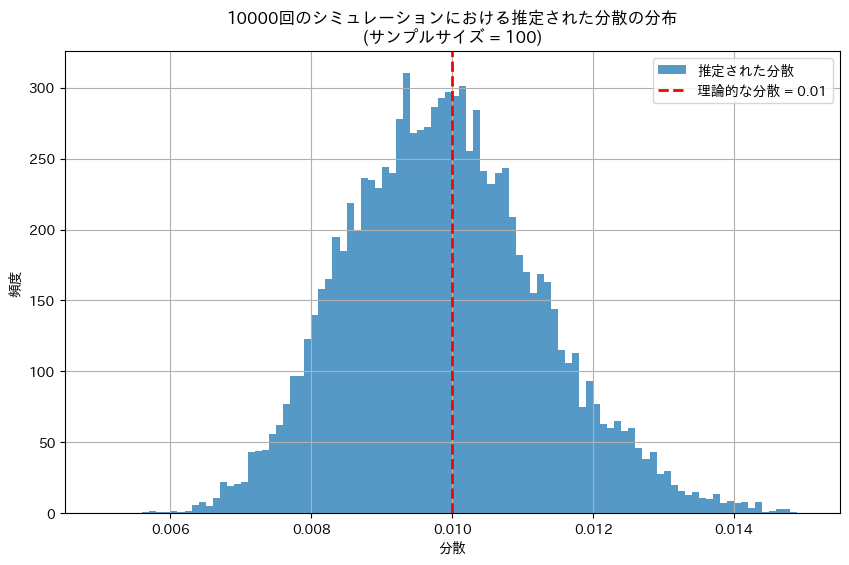
(2) 2変数の差の3乗の期待値
# 2021 Q4(1) 2024.8.31
import numpy as np
# パラメータの設定
n_simulations = 10000 # シミュレーション回数
mu = 0 # 平均
sigma = 1 # 標準偏差
# X1, X2を正規分布から生成
X1 = np.random.normal(loc=mu, scale=sigma, size=n_simulations)
X2 = np.random.normal(loc=mu, scale=sigma, size=n_simulations)
# (X1 - X2)^3を計算
expression = (X1 - X2)**3
# 期待値を計算
expected_value = np.mean(expression)
print(f"(X1 - X2)^3 の期待値: {expected_value}")(X1 - X2)^3 の期待値: 0.044962030052379295分布を見てみます
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 10000 # シミュレーション回数
mu = 0 # 平均
sigma = 1 # 標準偏差
# (X1 - X2)^3 の推定値を格納するリスト
expected_values = []
for _ in range(n):
# 正規分布に従う X1, X2 を生成
X1 = np.random.normal(loc=mu, scale=sigma)
X2 = np.random.normal(loc=mu, scale=sigma)
# (X1 - X2)^3 を計算
value = (X1 - X2)**3
expected_values.append(value)
# 理論的な期待値
theoretical_expectation = 0
# 視覚化
plt.figure(figsize=(10, 6))
plt.hist(expected_values, bins=100, alpha=0.75, label='(X1 - X2)^3 の推定値', range=(-30, 30))
plt.axvline(theoretical_expectation, color='red', linestyle='dashed', linewidth=2, label=f'理論的な期待値 = {theoretical_expectation}')
plt.xlabel('値')
plt.ylabel('頻度')
plt.title(f'{n}回のシミュレーションにおける (X1 - X2)^3 の期待値の分布')
plt.legend()
plt.grid(True)
plt.show()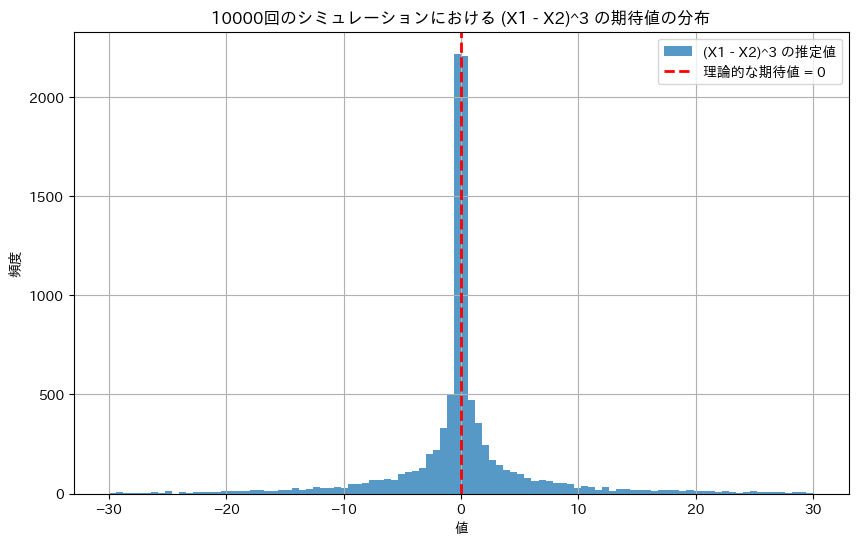
|X1-X2|が1より小さい場合は0付近に集中し、|X1-X2|が1より大きい場合は、三乗によって値が急激に増減する。分布は中心が尖って、左右対称になる。外れ値の影響を受けやすい。