ホーム » コードあり » 2014 Q5(1)

投稿一覧

2014 Q5(1)

投稿者: in コードあり, 二項分布, 多項分布, 最尤推定, 統計検定1級 2014年 統計数理 投稿日: 最終更新日:

テレビ番組の視聴満足回数の調査で満足と答えた回数のそれぞれ人数との組みが多項分布に従うのを利用し多項確率を構成する二項分布の確率pの最尤推定量を求めました。

　

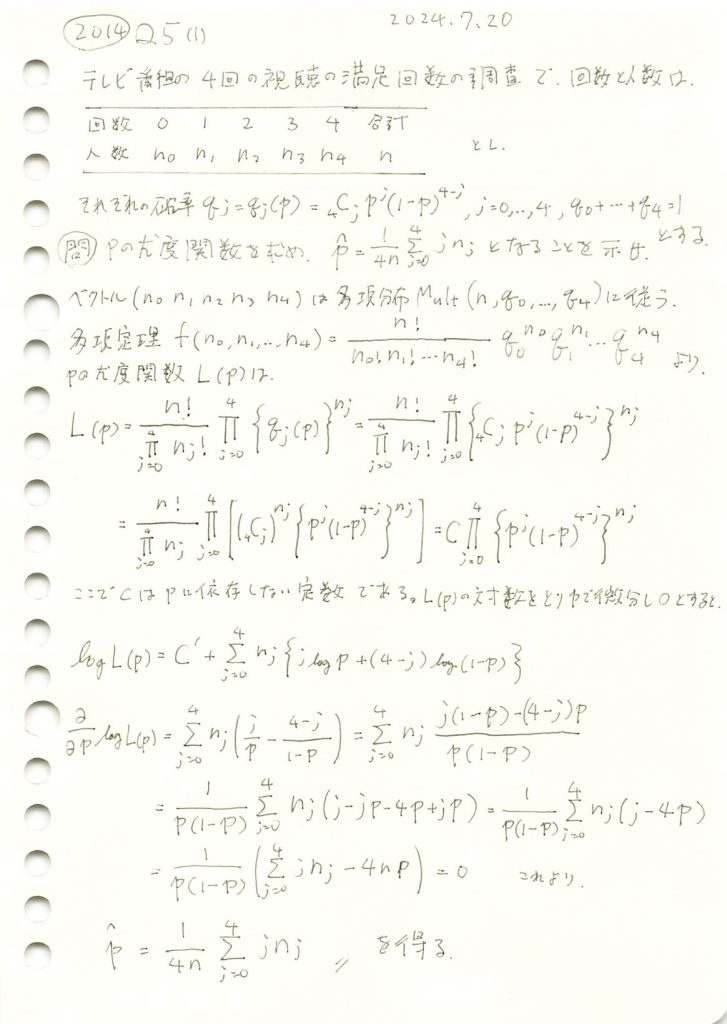
コード

真の確率pに基づいてシミュレーションを行い、最尤推定値\hat{p} = \frac{1}{4n} \sum_{j=0}^4 j n_jを計算し、真の確率pと比較します。

# 2014 Q5(1)  2025.1.15

import numpy as np
import matplotlib.pyplot as plt

# シミュレーションのパラメータ
n_simulations = 10000  # シミュレーション回数
n = 100  # 調査対象の人数
p_true = 0.6  # 真の満足確率

# nj のシミュレーション (j = 0, 1, 2, 3, 4)
data = np.random.binomial(4, p_true, size=n_simulations * n).reshape(n_simulations, n)

# 各シミュレーションでの最尤推定値を計算
p_estimates = np.sum(data, axis=1) / (4 * n)

# 平均値（推定されたp^の期待値）を計算
mean_p_estimate = np.mean(p_estimates)

# 推定されたp^の平均値と真の値を出力
print(f"推定された最尤推定値の平均: {mean_p_estimate:.4f}")
print(f"真の値: {p_true:.4f}")

# グラフの描画
plt.hist(p_estimates, bins=30, density=True, alpha=0.75, label="推定された $\\hat{p}$")
plt.axvline(p_true, color='red', linestyle='dashed', label=f"真の値 $p = {p_true}$")
plt.xlabel("推定された $\\hat{p}$")
plt.ylabel("密度")
plt.title("最尤推定値 $\\hat{p}$ の分布")
plt.legend()
plt.grid(alpha=0.5)
plt.show()
推定された最尤推定値の平均: 0.5997
真の値: 0.6000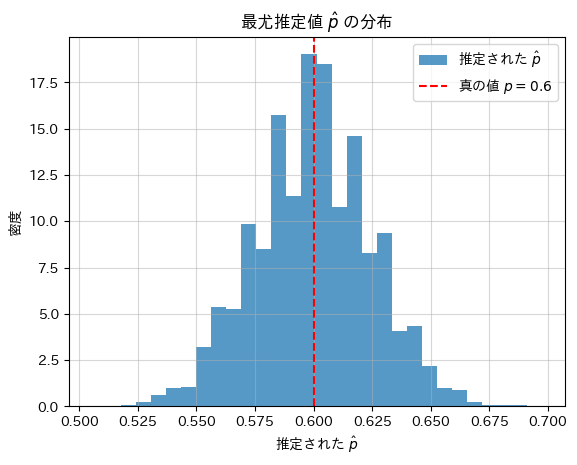

シミュレーションの結果、最尤推定値\hat{p} = \frac{1}{4n} \sum_{j=0}^4 j n_jは、真の確率pに近い値を示しました。