n個の一様分布の順序統計量の期待値を求めました。
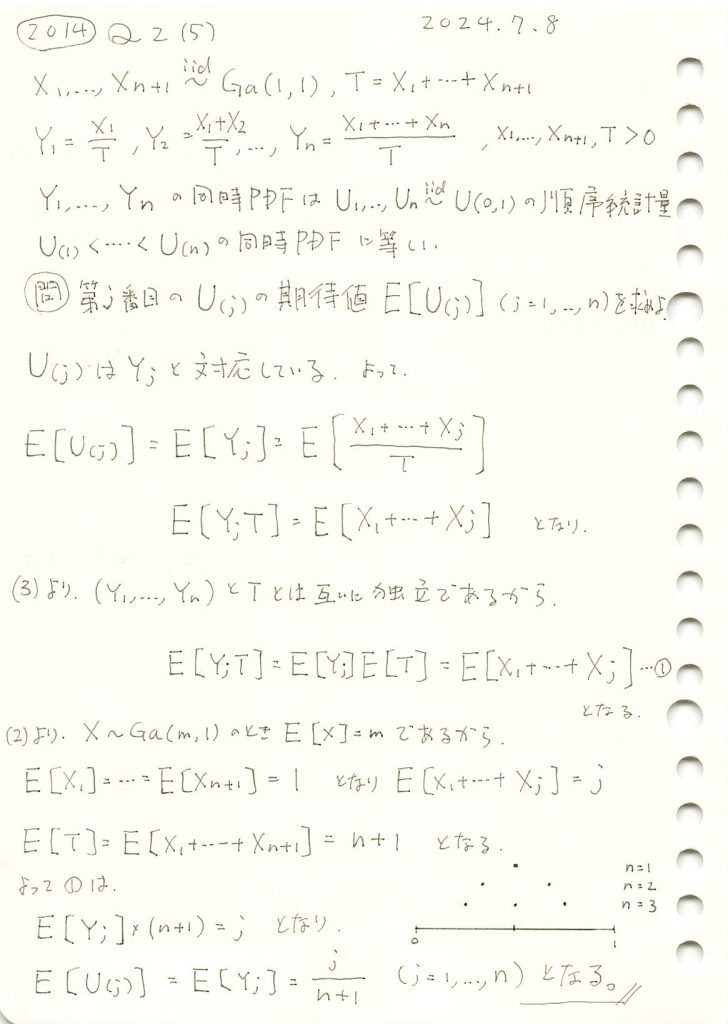
コード
サンプルサイズn=5として、一様分布の順序統計量![]() をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
# 2014 Q2(5) 2024.1.4
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_simulations = 10**6 # サンプルサイズ
n = 5 # サンプルサイズ (n個の確率変数)
# 一様分布からサンプリング
U = np.random.uniform(0, 1, (n_simulations, n))
# PDF (確率密度関数) および期待値をプロット
j_values = range(1, n + 1) # j を 1 から n まで変化させる
plt.figure(figsize=(14, 8))
colors = ['blue', 'orange', 'green', 'red', 'purple'] # 色の設定
for idx, j in enumerate(j_values):
# j 番目の順序統計量を取得
U_j = np.sort(U, axis=1)[:, j-1]
# 理論値のPDFを計算
u = np.linspace(0, 1, 1000)
pdf_theory = (n * np.math.comb(n-1, j-1)) * (u**(j-1)) * ((1-u)**(n-j))
# ヒストグラム (シミュレーション結果)
plt.hist(U_j, bins=50, density=True, alpha=0.5, label=f'j = {j} (シミュレーション)', color=colors[idx])
# 理論値のPDFをプロット
plt.plot(u, pdf_theory, linestyle='--', color=colors[idx], label=f'j = {j} (理論)')
# 理論値の期待値を直線で追加
expected_value = j / (n + 1)
plt.axvline(x=expected_value, color=colors[idx], linestyle=':', label=f'j = {j} 期待値 = {expected_value:.2f}')
# グラフ装飾
plt.title('順序統計量 U_(j) の PDF と期待値 (理論 vs シミュレーション)', fontsize=16)
plt.xlabel('値', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()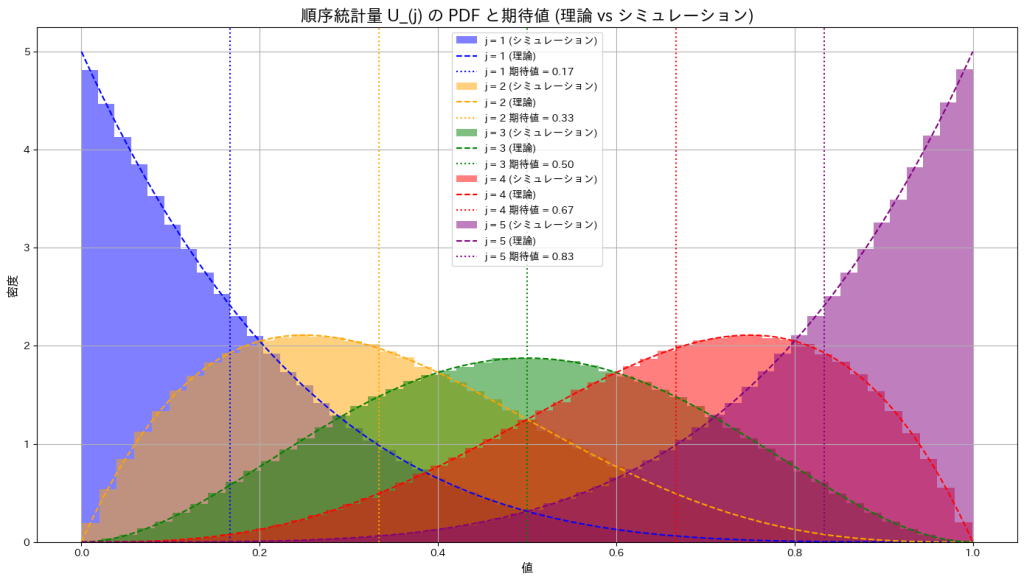
一様分布の順序統計量![]() の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。
の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。