ガンマ分布の平均と分散をモーメント母関数から求めました。
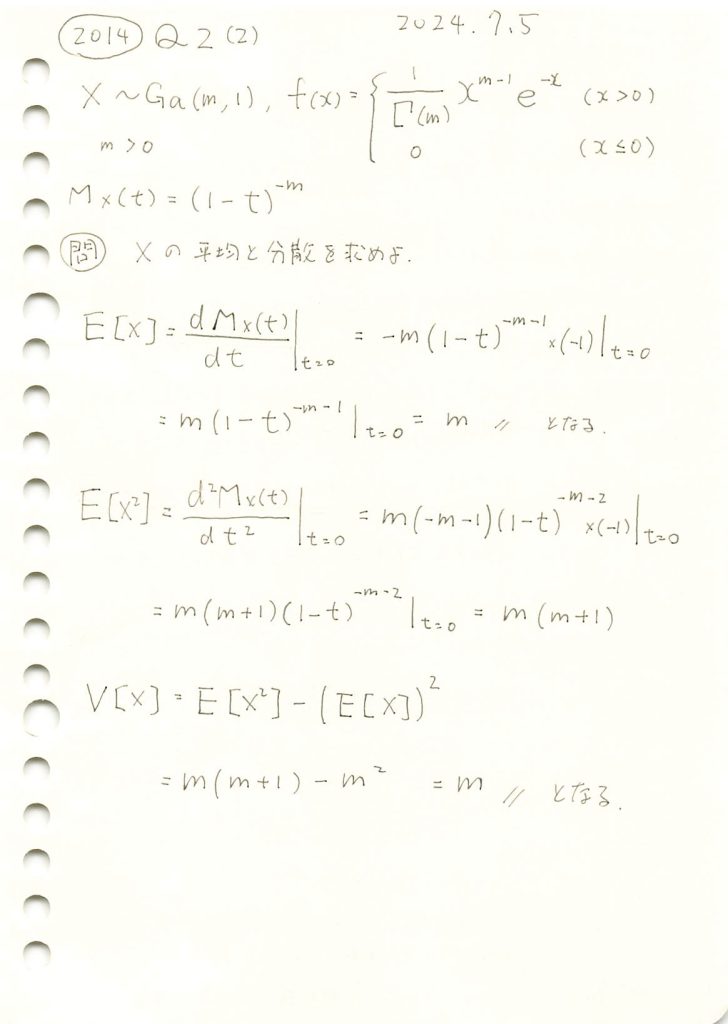
コード
形状パラメータm、スケールパラメータ1のガンマ分布について、期待値と分散が共にmになる様子をシミュレーションで確認し、確率密度の形を視覚的に確かめます。
# 2014 Q2(2) 2025.1.1
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ m の値を変化させる
m_values = [1, 2, 5, 10] # ガンマ分布の形状パラメータ
colors = ["blue", "orange", "green", "red"] # 各 m に対応する色
x = np.linspace(0, 20, 1000) # x の範囲
num_samples = 10000 # シミュレーションで生成する乱数の数
# グラフの描画
plt.figure(figsize=(12, 8))
for m, color in zip(m_values, colors):
# ガンマ分布の確率密度関数 (PDF)
pdf = gamma.pdf(x, a=m, scale=1) # a=m, scale=1 に対応
# 乱数生成
random_samples = gamma.rvs(a=m, scale=1, size=num_samples)
# ヒストグラムを描画
plt.hist(random_samples, bins=50, density=True, alpha=0.5, color=color, label=f"ヒストグラム (m={m})")
# PDF を描画
plt.plot(x, pdf, color=color, linewidth=2, label=f"PDF (m={m})")
# 期待値の線
mean = m # ガンマ分布の期待値
plt.axvline(mean, color=color, linestyle="--", alpha=0.7, label=f"期待値 (m={m})")
# グラフの装飾
plt.title("ガンマ分布のPDFとシミュレーションによるヒストグラム", fontsize=16)
plt.xlabel("$x$", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()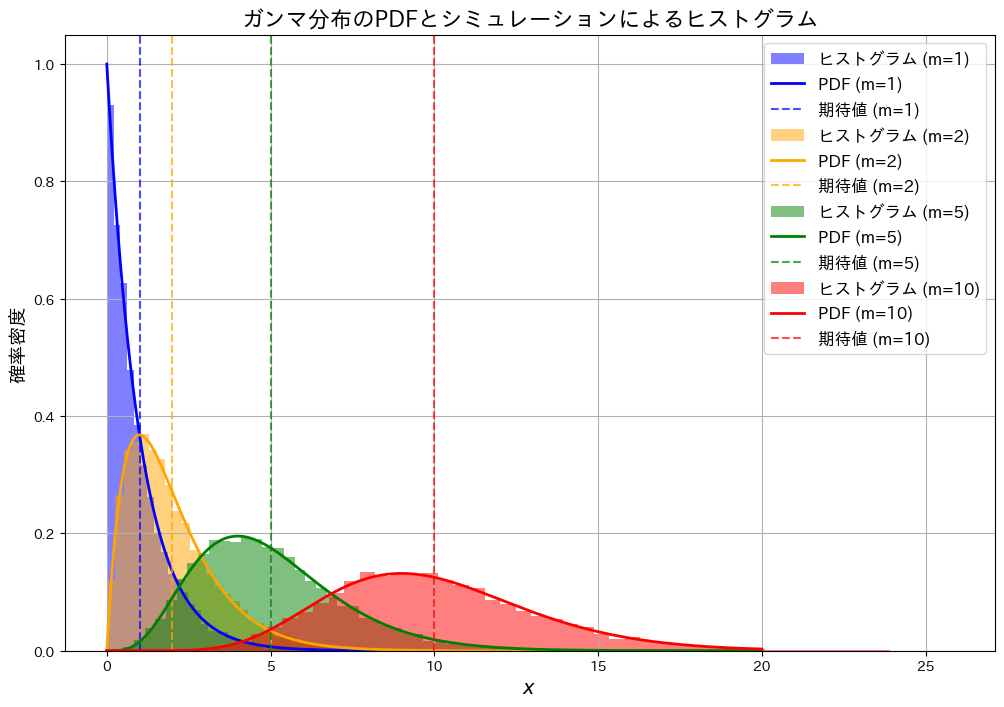
形状パラメータmと期待値が一致し、また、mが大きくなるにつれて分布が広がっている様子が確認できました。分散がmになることを直接確認していませんが、分布の広がりがmと連動していることが示唆されています。