2021 Q3(1)
ポアソン分布のモーメント母関数を求めました。
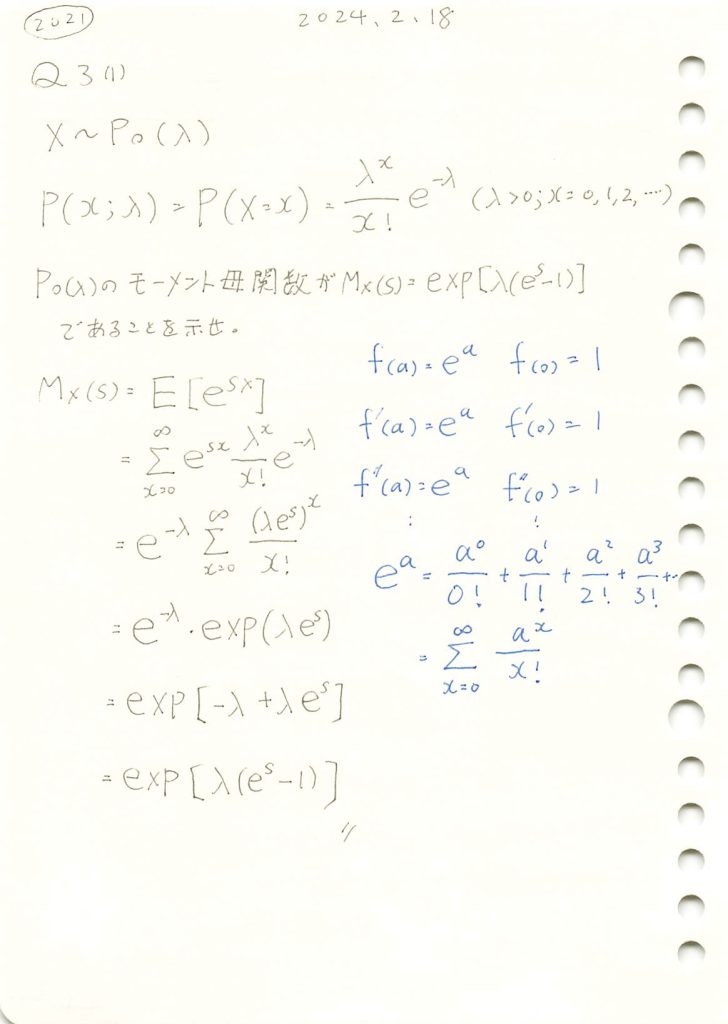
コード
数式を使った計算
# 2021 Q3(1) 2024.8.25
import sympy as sp
# 変数の定義
s, x, lambda_ = sp.symbols('s x lambda_', real=True, positive=True)
# ポアソン分布の確率質量関数 (PMF)
poisson_pmf = (lambda_**x * sp.exp(-lambda_)) / sp.factorial(x)
# モーメント母関数 M_X(s) の定義
M_X = sp.summation(sp.exp(s*x) * poisson_pmf, (x, 0, sp.oo))
# 結果を簡略化
M_X_simplified = sp.simplify(M_X)
# 結果を表示
M_X_simplified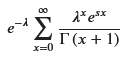
無限級数がe^xの形に変換されないようです。
exp(s) を t に置き換えて、最後に戻してみます。
# 2021 Q3(1) 2024.8.25
import sympy as sp
# 変数の定義
s, x, lambda_, t = sp.symbols('s x lambda_ t', real=True, positive=True)
# exp(s) を t に置き換え
summand = (lambda_ * t)**x / sp.factorial(x)
# モーメント母関数 M_X(s) の定義
M_X = sp.exp(-lambda_) * sp.summation(summand, (x, 0, sp.oo))
# 簡略化
M_X_simplified = sp.simplify(M_X)
# 最後に t を exp(s) に戻す
M_X_final = M_X_simplified.subs(t, sp.exp(s))
# 結果を表示
M_X_final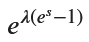
手計算と同じ形になりました。
モーメント母関数を使って期待値と分散を求めます。
import sympy as sp
# 変数の定義
s, lambda_ = sp.symbols('s lambda_', real=True, positive=True)
# モーメント母関数 M_X(s) の定義
M_X = sp.exp(lambda_ * (sp.exp(s) - 1))
# 1次モーメント(期待値)の計算
M_X_prime = sp.diff(M_X, s)
expectation = M_X_prime.subs(s, 0)
# 2次モーメントの計算
M_X_double_prime = sp.diff(M_X_prime, s)
second_moment = M_X_double_prime.subs(s, 0)
# 分散の計算
variance = second_moment - expectation**2
# 結果を表示
display(expectation, variance)
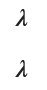
2021 Q2(4)
事前分布と尤度から事後確率が最大となるパラメータの推定値を求めました。

コード
数式を使った計算
# 2021 Q2(4) 2024.8.24
import numpy as np
from scipy.special import comb
# 事前分布 P(N_A)
def prior(NA):
return NA + 1
# 尤度関数 P(X = 4 | N_A)
def likelihood(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# 事後分布 P(N_A | X = 4) (正規化定数は省略)
def posterior(NA):
return prior(NA) * likelihood(NA)
# N_A の範囲
NA_values = np.arange(4, 90)
# 事後分布の計算
posterior_values = [posterior(NA) for NA in NA_values]
# 最大値を取る N_A (事後モード) を探索
NA_mode = NA_values[np.argmax(posterior_values)]
NA_mode30プロット
# 2021 Q2(4) 2024.8.24
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 事前分布 P(N_A)
def prior(NA):
return NA + 1
# 正規化定数
C = 1 / 5151
# 尤度関数 P(X = 4 | N_A)
def likelihood(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# 事後分布 P(N_A | X = 4)
def posterior(NA):
return prior(NA) * likelihood(NA)
# N_A の範囲を0から100まで(事前分布用)
NA_values_full = np.arange(0, 101)
# 事前分布を計算(0から100まで)
prior_values_full = [C * prior(NA) for NA in NA_values_full]
# N_A の範囲を4から89まで(事後分布用)
NA_values = np.arange(4, 90)
# 事後分布の計算
posterior_values = [posterior(NA) for NA in NA_values]
# 事後分布の正規化
posterior_sum = sum(posterior_values)
posterior_values_normalized = [value / posterior_sum for value in posterior_values]
# 事前分布が存在しない場合の事後分布(尤度のみを正規化)
likelihood_values = [likelihood(NA) for NA in NA_values]
likelihood_sum = sum(likelihood_values)
likelihood_values_normalized = [value / likelihood_sum for value in likelihood_values]
# 3つの分布を重ねて表示
plt.figure(figsize=(10, 6))
# 事前分布のプロット(0から100まで)
plt.plot(NA_values_full, prior_values_full, 'g-', label=r'事前分布 $P(N_A)$', markersize=5)
# 事後分布のプロット(4から89まで)
plt.plot(NA_values, posterior_values_normalized, 'bo-', label=r'事後分布 $P(N_A | X = 4)$', markersize=5)
# 事前分布が存在しない場合の事後分布(尤度のみ)
plt.plot(NA_values, likelihood_values_normalized, 'r-', label=r'事前分布なし $P(N_A | X = 4)$', markersize=5)
# 事後モードのプロット
NA_mode = NA_values[np.argmax(posterior_values_normalized)]
plt.axvline(NA_mode, color='blue', linestyle='--', label=f'事後モード: {NA_mode}')
# 事前分布なしの場合の最尤推定値のプロット
NA_mode_likelihood = NA_values[np.argmax(likelihood_values_normalized)]
plt.axvline(NA_mode_likelihood, color='red', linestyle=':', label=f'最尤推定値 (事前分布なし): {NA_mode_likelihood}')
# グラフの設定
plt.xlabel(r'$N_A$')
plt.ylabel(r'確率')
plt.title(r'事前分布ありとなしの比較')
plt.grid(True)
plt.legend()
plt.show()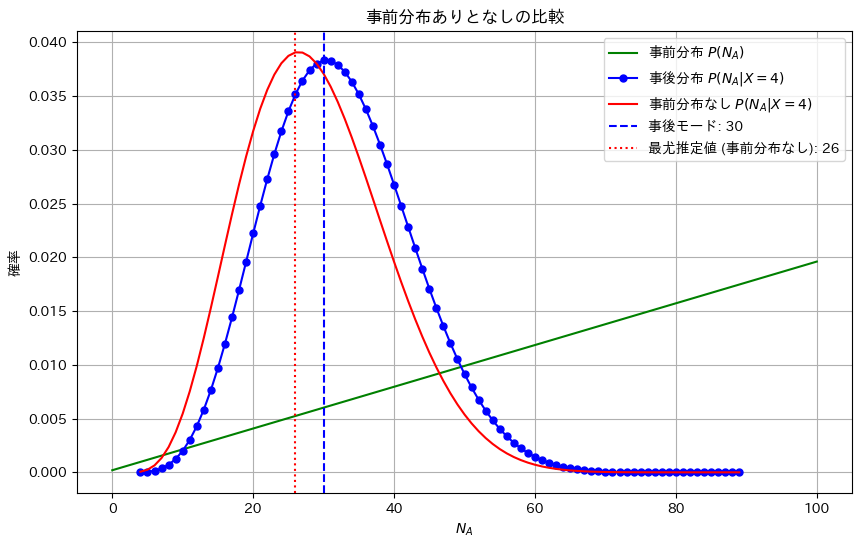
2021 Q2(3)
離散型確率分布の正規化定数を計算しました。

コード
数式を使った計算
# 2021 Q2(3) 2024.8.23
from sympy import symbols, summation, Eq, solve
# 記号の定義
n = symbols('n', integer=True)
C = symbols('C', real=True)
# 和を計算
sum_expr = summation(C * (n + 1), (n, 0, 100))
# 正規化条件を設定
normalization_condition = Eq(sum_expr, 1)
# C を解く
C_value = solve(normalization_condition, C)[0]
C_value
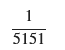
P(N_A = n)のプロット
# 2021 Q2(3) 2024.8.23
import matplotlib.pyplot as plt
import numpy as np
# 正規化定数 C
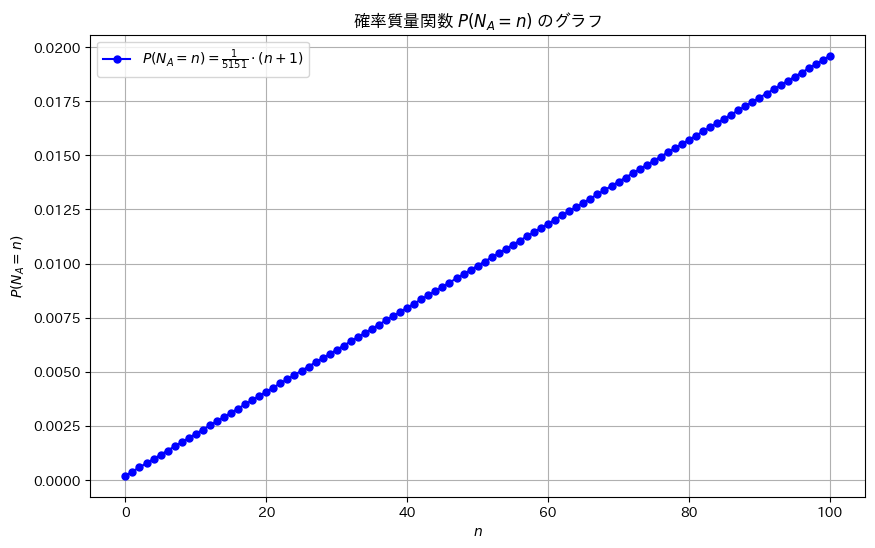
C_value = 1 / 5151
# n の範囲
n_values = np.arange(0, 101)
# 確率質量関数 P(N_A = n)
pmf_values = C_value * (n_values + 1)
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(n_values, pmf_values, 'bo-', label=r'$P(N_A = n) = \frac{1}{5151} \cdot (n + 1)$', markersize=5)
plt.xlabel(r'$n$')
plt.ylabel(r'$P(N_A = n)$')
plt.title(r'確率質量関数 $P(N_A = n)$ のグラフ')
plt.grid(True)
plt.legend()
plt.show()
2021 Q2(2)
超幾何分布の当たりの数の推定値を尤度比を使って求めました。

コード
シミュレーションによる計算
# 2021 Q2(2) 2024.8.22
import numpy as np
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# L(N_A + 1) / L(N_A) を計算し、条件を満たす最小の N_A を探索
# max(0, N_A - 85) ≤ 4 ≤ min(15, N_A) の式に基づき、取り出した豆Aが4粒の場合の N_A の範囲を設定 (4 ≤ N_A ≤ 89)
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
NA_optimal = NA_values[np.where(np.array(ratios) < 1)[0][0]]
print(f"L(N_A + 1) / L(N_A) < 1 となる最小の N_A は {NA_optimal} です。")
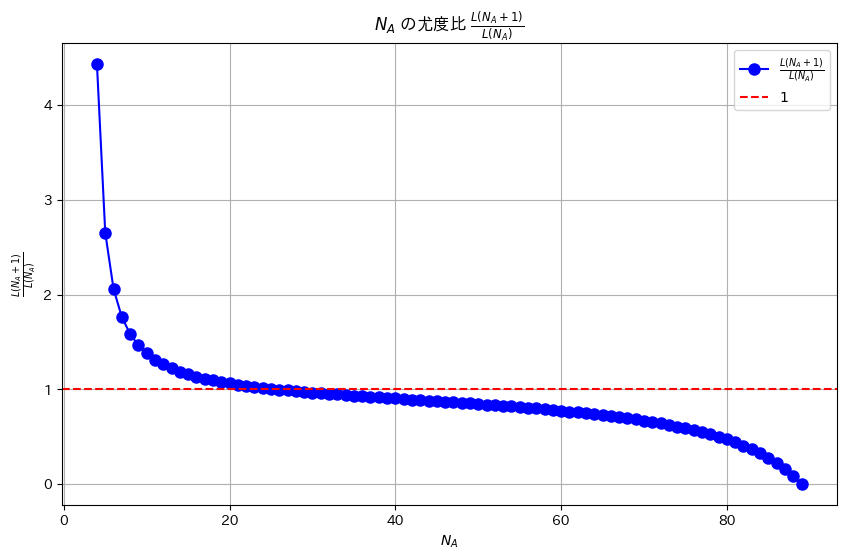
L(N_A + 1) / L(N_A) < 1 となる最小の N_A は 26 です。プロット
# 2021 Q2(2) 2024.8.22
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# N_A の範囲を設定
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(NA_values, ratios, 'bo-', label=r'$\frac{L(N_A + 1)}{L(N_A)}$', markersize=8)
plt.axhline(y=1, color='red', linestyle='--', label=r'$1$')
plt.xlabel(r'$N_A$')
plt.ylabel(r'$\frac{L(N_A + 1)}{L(N_A)}$')
plt.title(r'$N_A$ の尤度比 $\frac{L(N_A + 1)}{L(N_A)}$')
plt.legend()
plt.grid(True)
plt.show()
プロット(NA=26付近をズーム)
# 2021 Q2(2) 2024.8.22
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# N_A の範囲を設定
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
# 26付近のズームしたグラフを描画
plt.figure(figsize=(10, 6))
plt.plot(NA_values, ratios, 'bo-', label=r'$\frac{L(N_A + 1)}{L(N_A)}$', markersize=8)
plt.axhline(y=1, color='red', linestyle='--', label=r'$1$')
plt.xlabel(r'$N_A$')
plt.ylabel(r'$\frac{L(N_A + 1)}{L(N_A)}$')
plt.title(r'$N_A$ の尤度比 $\frac{L(N_A + 1)}{L(N_A)}$ (25 < $N_A$ < 30)')
plt.xlim(25, 30) # N_A = 26 付近をズーム
plt.ylim(0.95, 1.05) # y軸もズームして見やすく
plt.legend()
plt.grid(True)
plt.show()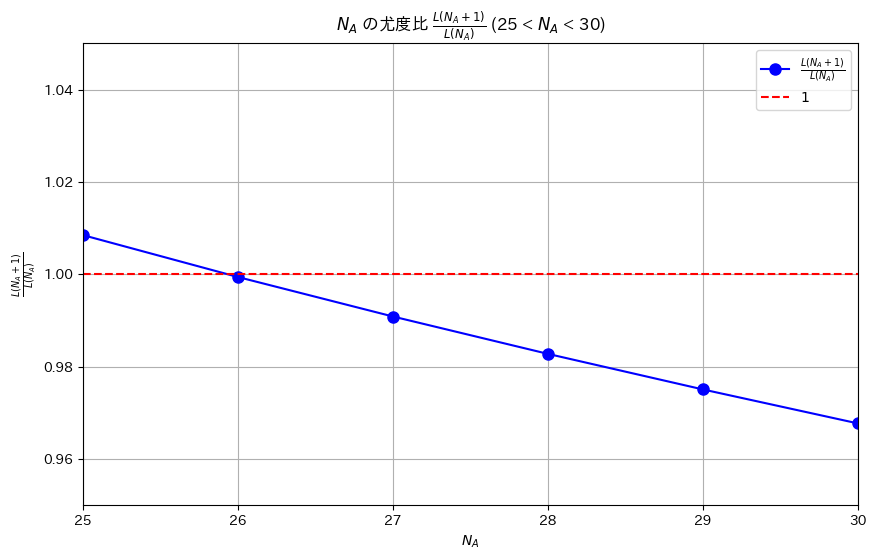
2021 Q2(1)
超幾何分布の問題をやりました。

コード
シミュレーションによる計算
# 2021 Q2(1) 2024.8.21
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import hypergeom
# パラメータの設定
M = 100 # 全体の豆の数
N_A = 30 # 豆Aの数
n = 15 # 抽出する豆の数
x_values = np.arange(0, n+1) # 可能な豆Aの数
# 理論的な超幾何分布のPMFを計算
rv = hypergeom(M, N_A, n)
pmf_theoretical = rv.pmf(x_values)
# 数値シミュレーションの設定
n_simulations = 10000 # シミュレーション回数
simulated_counts = []
# シミュレーションの実行
for _ in range(n_simulations):
# 袋の中の豆を表すリスト(1が豆A、0が豆B)
bag = np.array([1]*N_A + [0]*(M - N_A))
# 無作為に15個抽出
sample = np.random.choice(bag, size=n, replace=False)
# 抽出した中の豆Aの数をカウント
count_A = np.sum(sample)
simulated_counts.append(count_A)
# シミュレーションから得られたPMFを計算
pmf_simulated, bins = np.histogram(simulated_counts, bins=np.arange(-0.5, n+1.5, 1), density=True)
# グラフの描画
plt.figure(figsize=(10, 6))
# 理論的なPMFの描画
plt.plot(x_values, pmf_theoretical, 'bo-', label='理論的PMF', markersize=8)
# シミュレーション結果をヒストグラムとして描画
plt.hist(simulated_counts, bins=np.arange(-0.5, n+1.5, 1), density=True, alpha=0.5, color='red', label='シミュレーション結果')
# グラフの設定
plt.xlabel('豆Aの数')
plt.ylabel('確率')
plt.title('超幾何分布のPMF: 理論とシミュレーションの比較')
plt.legend()
plt.grid(True)
plt.show()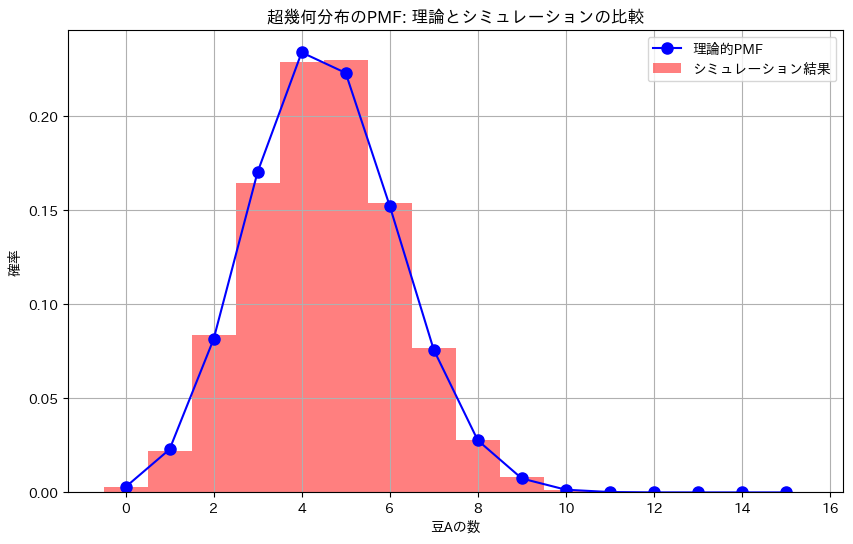
2021 Q1(4)
独立ではない2つの確率変数の積の期待値を求めました。

コード
数式を使った計算
# 2021 Q1(4) 2024.8.20
import sympy as sp
# シンボリック変数の定義
x, y = sp.symbols('x y')
# h(x) の導出
h_x = sp.integrate(sp.exp(-x), (x, 0, x))
# XY の期待値の計算
# h(x) = 1 - exp(-x) を使って E[X * h(X)] を計算する
integral_part1 = sp.integrate(x * h_x * sp.exp(-x), (x, 0, sp.oo))
E_XY_simplified = sp.simplify(integral_part1)
# 結果の表示
display(sp.Eq(sp.Symbol('h(x)'), h_x))
display(sp.Eq(sp.Symbol('E[XY]'), E_XY_simplified))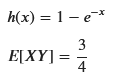
指数分布に従う乱数Xを生成し、Y=h(X)Yが一様分布に従うか確認
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
num_samples = 100000 # サンプル数
# 指数分布に従う乱数 X を生成
X_samples = np.random.exponential(scale=1.0, size=num_samples)
# 関数 Y = h(X) = 1 - exp(-X) を適用して Y を計算
Y_samples = 1 - np.exp(-X_samples)
# ヒストグラムのプロット
plt.figure(figsize=(8, 5))
plt.hist(Y_samples, bins=50, density=True, alpha=0.6, color='g', label='シミュレーションされた Y=h(X)')
plt.xlabel('y')
plt.ylabel('密度')
plt.title('Y = h(X) の分布 (シミュレーション結果)')
plt.legend()
plt.grid(True)
plt.show()
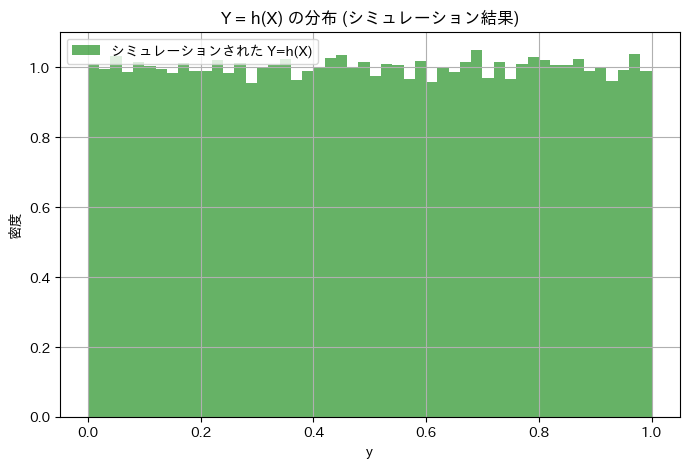
シミュレーションによるE[XY]の計算
import numpy as np
# シミュレーションの設定
num_samples = 100000 # サンプル数
# 指数分布に従う乱数 X を生成
X_samples = np.random.exponential(scale=1.0, size=num_samples)
# 関数 Y = h(X) = 1 - exp(-X) を適用して Y を計算
Y_samples = 1 - np.exp(-X_samples)
# XY の期待値を計算
XY_samples = X_samples * Y_samples
E_XY_simulation = np.mean(XY_samples)
# 結果の表示
print(f"シミュレーションによる E[XY] = {E_XY_simulation}")
print(f"理論値 E[XY] = 3/4 = {3/4}")シミュレーションによる E[XY] = 0.7473462073557277
理論値 E[XY] = 3/4 = 0.752024 Q1(3)
変数変換を用いて二つの分布の和の確率密度関数を求めました。

コード
数式を使った計算
# 2024 Q1(3) 2024.8.19
import sympy as sp
# シンボリック変数の定義
x, z = sp.symbols('x z')
# 確率密度関数の定義
f_X = sp.exp(-x) # f_X(x) = e^(-x)
f_Y = sp.Piecewise((1, (z - x >= 0) & (z - x <= 1)), (0, True)) # f_Y(z - x) for 0 < z - x < 1
# 一般的な積分の設定
f_Z_integral = sp.integrate(f_X * f_Y, (x, 0, z))
# 結果の簡略化
f_Z_general = sp.simplify(f_Z_integral)
# 結果の表示
display(f_Z_general)
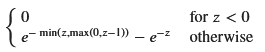
簡単のため、zの範囲を指定して再度計算
# 2024 Q1(3) 2024.8.19
import sympy as sp
# シンボリック変数の定義
x, z = sp.symbols('x z')
# 確率密度関数の定義
f_X = sp.exp(-x) # f_X(x) = e^(-x)
f_Y = 1 # f_Y(y) = 1 (0 < y < 1)
# 各範囲での計算
# 1. z <= 0 の場合
f_Z_1 = 0 # z <= 0 の場合は f_Z(z) = 0
# 2. 0 < z <= 1 の場合
f_Z_2_integral = sp.integrate(f_X * f_Y, (x, 0, z))
f_Z_2 = sp.simplify(f_Z_2_integral)
# 3. z > 1 の場合
f_Z_3_integral = sp.integrate(f_X * f_Y, (x, z-1, z))
f_Z_3 = sp.simplify(f_Z_3_integral)
# 結果の表示
print(f"f_Z(z) for z <= 0:")
display(f_Z_1)
print(f"f_Z(z) for 0 < z <= 1:")
display(f_Z_2)
print(f"f_Z(z) for z > 1:")
display(f_Z_3)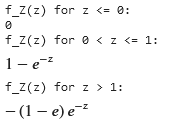
プロット
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
# 確率密度関数 f_X(x) と f_Y(y)
def f_X(x):
return np.exp(-x) if x > 0 else 0
def f_Y(y):
return 1 if 0 < y < 1 else 0
# Z = X + Y の確率密度関数 f_Z(z) の計算
def f_Z(z):
integrand = lambda x: f_X(x) * f_Y(z - x)
return quad(integrand, max(0, z-1), z)[0] #積分範囲を限定する場合
#return quad(integrand, 0, z, epsabs=1e-8, epsrel=1e-8)[0] #積分範囲を広くする場合
# z の範囲を設定し、f_Z(z) を計算
z_values = np.linspace(0, 5, 1000) # 増加させたサンプル数
f_Z_values = np.array([f_Z(z) for z in z_values])
# グラフの描画
plt.plot(z_values, f_Z_values, label='f_Z(z) = X + Y')
plt.xlabel('z')
plt.ylabel('確率密度')
plt.title('X + Y の確率密度関数')
plt.legend()
plt.grid(True)
plt.show()
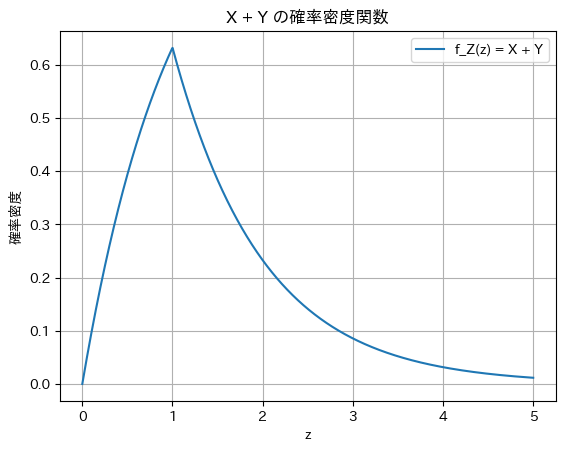
2021 Q1(1)(2)
指数分布と一様分布の期待値と、それらが独立な場合の積の期待値を求めました。
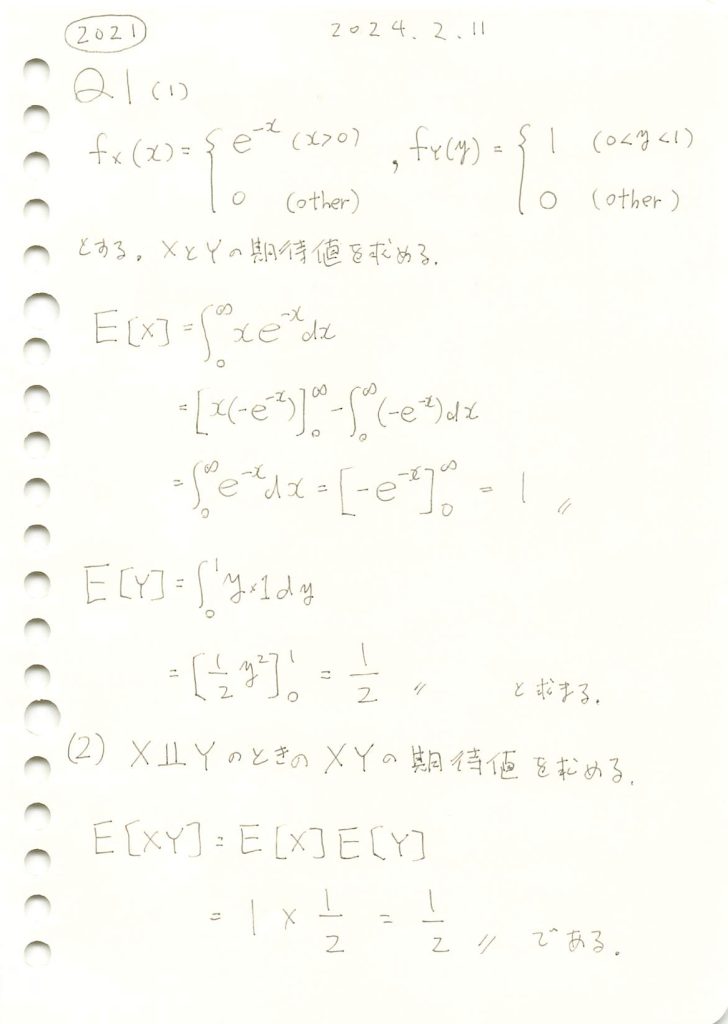
コード
数式を使った計算
# 2021 Q1(1)(2) 2024.8.18
import numpy as np
from scipy.integrate import quad
# Xの期待値の計算
def fx(x):
return x * np.exp(-x)
E_X, _ = quad(fx, 0, np.inf)
# Yの期待値の計算
def fy(y):
return y
E_Y, _ = quad(fy, 0, 1)
# XYの期待値の計算(独立の場合)
E_XY = E_X * E_Y
print(f"E[X] = {E_X}")
print(f"E[Y] = {E_Y}")
print(f"E[XY] (独立の場合) = {E_XY}")
E[X] = 0.9999999999999998
E[Y] = 0.5
E[XY] (独立の場合) = 0.4999999999999999シミュレーションによる計算
# 2021 Q1(1)(2) 2024.8.18
import numpy as np
# シミュレーションの設定
num_samples = 1000000 # サンプル数
# Xの乱数生成(指数分布)
X_samples = np.random.exponential(scale=1.0, size=num_samples)
# Yの乱数生成(一様分布)
Y_samples = np.random.uniform(0, 1, size=num_samples)
# (1) XとYの期待値の計算
E_X_simulation = np.mean(X_samples)
E_Y_simulation = np.mean(Y_samples)
# (2) XYの期待値の計算(独立な場合)
E_XY_simulation = np.mean(X_samples * Y_samples)
print(f"E[X] = {E_X_simulation}")
print(f"E[Y] = {E_Y_simulation}")
print(f"E[XY] = {E_XY_simulation}")
E[X] = 1.0001064255963075
E[Y] = 0.4998284579940602
E[XY] = 0.49980383195826882022 Q5(5)
欠損値がある場合の、分散分析に於けるF検定の影響に関する問をもう一問やりました。

コード
シミュレーションによる計算
# 2022 Q5(5) 2024.8.17
import numpy as np
# シミュレーションの設定
np.random.seed(42)
n = 5 # サンプル数
X = np.random.normal(10, 2, n) # Xの観測値
# Y1が非常に大きな値を取るケースを考慮
Y = np.random.normal(15, 2, n)
Y[0] = 1000 # Y1が非常に大きな値を取る設定
# 全体平均とY2:nの平均
Y_bar = np.mean(Y) # 全体の平均
Y_bar_2n = np.mean(Y[1:]) # Y2:n の平均
X_bar_2n = np.mean(X[1:]) # X2:n の平均
# θの推定値
theta_hat = Y_bar_2n - X_bar_2n
# SAの計算(Y1を含める場合)
SA_with_Y1 = np.sum(((X[1:] + Y[1:] - theta_hat) / 2 - X_bar_2n) ** 2) + (Y[0] - Y_bar) ** 2
SA_with_Y1 += np.sum(((X[1:] + Y[1:] + theta_hat) / 2 - Y_bar) ** 2)
# SAの計算(Y1を除く場合)
SA_without_Y1 = np.sum(((X[1:] + Y[1:] - theta_hat) / 2 - X_bar_2n) ** 2)
SA_without_Y1 += np.sum(((X[1:] + Y[1:] + theta_hat) / 2 - Y_bar_2n) ** 2)
# 結果を表示
{
"Y1を含めた場合の要因A平方和 (SA)": SA_with_Y1,
"Y1を除いた場合の要因A平方和 (SA)": SA_without_Y1
}{'Y1を含めた場合の要因A平方和 (SA)': 774276.0933538243,
'Y1を除いた場合の要因A平方和 (SA)': 1.6720954914667048}