2022 Q3(5)
モーメント法によりガンマポアソン分布のパラメータの推定量を求めました。

コード
数式を使った計算
# 2022 Q3(5) 2024.8.6
from sympy import init_printing
from sympy import symbols, Eq, solve
# これでTexの表示ができる
init_printing()
# 変数の定義
r, p, X_bar, S_squared = symbols('r p X_bar S_squared')
alpha, beta = symbols('alpha beta')
# モーメント法の方程式を定義
# 期待値 E[X] にサンプル平均を一致させる
eq1_correct = Eq(X_bar, alpha / beta)
# 分散 V[X] にサンプル分散を一致させる
eq2_correct = Eq(S_squared, alpha / beta**2 + alpha / beta)
# 方程式を解いて α と β を求める
solutions_correct = solve((eq1_correct, eq2_correct), (alpha, beta))
solutions_correct
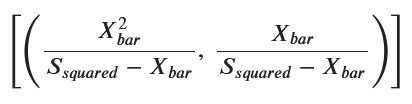
シミュレーションによる計算
# 2022 Q3(5) 2024.8.6
import numpy as np
from scipy.stats import nbinom
# 1. パラメータの設定
alpha_true = 3.0
beta_true = 2.0
# 2. 負の二項分布のパラメータ計算
r = alpha_true
p = beta_true / (beta_true + 1)
# 3. 負の二項分布から乱数を生成
sample_size = 10000
nbinom_samples = nbinom.rvs(r, p, size=sample_size)
# 4. サンプル統計量の計算
X_bar = np.mean(nbinom_samples)
S_squared = np.var(nbinom_samples, ddof=1)
# 5. モーメント法によるパラメータ推定
alpha_estimated = X_bar**2 / (S_squared - X_bar)
beta_estimated = X_bar / (S_squared - X_bar)
# 6. 推定結果の表示
print(f"推定された α: {alpha_estimated}")
print(f"推定された β: {beta_estimated}")
print(f"理論値 α: {alpha_true}")
print(f"理論値 β: {beta_true}")推定された α: 2.93536458612626
推定された β: 1.95157541794180
理論値 α: 3.0
理論値 β: 2.0アルゴリズム
シミュレーションによる計算
パラメータの設定:
- 真のパラメータ
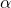 と
と 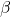 を設定する。
を設定する。
負の二項分布のパラメータ計算:
- パラメータ

- パラメータ
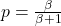
負の二項分布から乱数を生成:
- サンプルサイズ
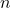 を設定し、負の二項分布から乱数を生成する。
を設定し、負の二項分布から乱数を生成する。
サンプル統計量の計算:
- サンプル平均
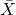 と分散
と分散 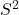 を計算する。
を計算する。
モーメント法によるパラメータ推定:
- 推定された
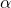 を
を 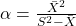 で計算する。
で計算する。 - 推定された
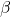 を
を 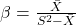 で計算する。
で計算する。
推定結果の表示:
- 推定された
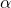 と
と 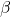 を表示する。
を表示する。 - 真の
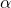 と
と 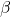 を表示する。
を表示する。
2022 Q3(4)
条件付き期待値の公式と条件付き分散の公式を使ってガンマポアソン分布の期待値と分散を求めました。

コード
数式を使った計算
# 2022 Q3(4) 2024.8.7
import sympy as sp
# 定義
k, lambda_var = sp.symbols('k lambda')
alpha, beta = sp.symbols('alpha beta', positive=True)
# ポアソン分布の確率質量関数
poisson_pmf = (lambda_var**k * sp.exp(-lambda_var)) / sp.factorial(k)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha - 1) * sp.exp(-beta * lambda_var)
# 周辺分布の計算
marginal_distribution = sp.integrate(poisson_pmf * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# 期待値 E[X] の計算
expected_value = sp.summation(k * marginal_distribution, (k, 0, sp.oo)).simplify()
# 分散 V[X] の計算
expected_value_of_square = sp.summation(k**2 * marginal_distribution, (k, 0, sp.oo)).simplify()
variance = (expected_value_of_square - expected_value**2).simplify()
# 結果を表示
results = {
"期待値 E[X]": expected_value,
"分散 V[X]": variance
}
results{'期待値 E[X]': alpha/beta, '分散 V[X]': alpha*(beta + 1)/beta**2}シミュレーションによる計算
import numpy as np
# パラメータの設定
alpha = 3.0
beta = 2.0
sample_size = 10000
# ガンマ分布から λ を生成
lambda_samples = np.random.gamma(alpha, 1/beta, sample_size)
# 生成された λ を使ってポアソン分布から X を生成
poisson_samples = [np.random.poisson(lam) for lam in lambda_samples]
# サンプルの期待値と分散を計算
sample_mean = np.mean(poisson_samples)
sample_variance = np.var(poisson_samples)
# 理論値を計算
theoretical_mean = alpha / beta
theoretical_variance = alpha * (beta + 1) / beta**2
# 結果を表示
results_with_caption = {
"シミュレーションによる期待値": sample_mean,
"理論値による期待値": theoretical_mean,
"シミュレーションによる分散": sample_variance,
"理論値による分散": theoretical_variance
}
results_with_caption{'シミュレーションによる期待値': 1.5027,
'理論値による期待値': 1.5,
'シミュレーションによる分散': 2.31159271,
'理論値による分散': 2.25}2022 Q3(3)
ポアソン分布のパラメータλがガンマ分布に従うと負の二項分布になる。

コード
数式を使った計算
# 2022 Q3(3) 2024.8.5
import sympy as sp
# 定義
k = sp.symbols('k', integer=True)
alpha, beta = sp.symbols('alpha beta', positive=True)
lambda_var = sp.symbols('lambda', positive=True)
# ポアソン分布の確率質量関数
poisson_pmf = (lambda_var**k * sp.exp(-lambda_var)) / sp.factorial(k)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha - 1) * sp.exp(-beta * lambda_var)
# 周辺分布の計算
marginal_distribution = sp.integrate(poisson_pmf * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
marginal_distribution
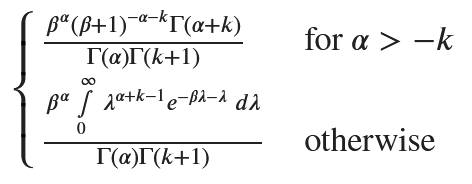
次式と同じなので、負の二項分布となる。
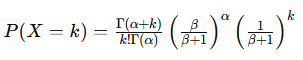
シミュレーションによる計算
# 2022 Q3(3) 2024.8.5
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma, nbinom
# パラメータの設定
alpha = 3.0
beta = 2.0
sample_size = 10000
# ガンマ分布から λ を生成
lambda_samples = np.random.gamma(alpha, 1/beta, sample_size)
# 生成された λ を使ってポアソン分布から X を生成
poisson_samples = [np.random.poisson(lam) for lam in lambda_samples]
# 負の二項分布のパラメータを設定
r = alpha
p = beta / (beta + 1)
# 負の二項分布から理論的な確率質量関数を計算
x = np.arange(0, max(poisson_samples) + 1)
nbinom_pmf = nbinom.pmf(x, r, p)
# ヒストグラムの描画
plt.hist(poisson_samples, bins=np.arange(0, max(poisson_samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black', rwidth=0.8)
# 理論的な負の二項分布の確率質量関数をプロット
plt.plot(x, nbinom_pmf, 'r', linestyle='-', label='理論的な負の二項分布')
# グラフのタイトルとラベル
plt.title('ポアソン-ガンマ混合分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()
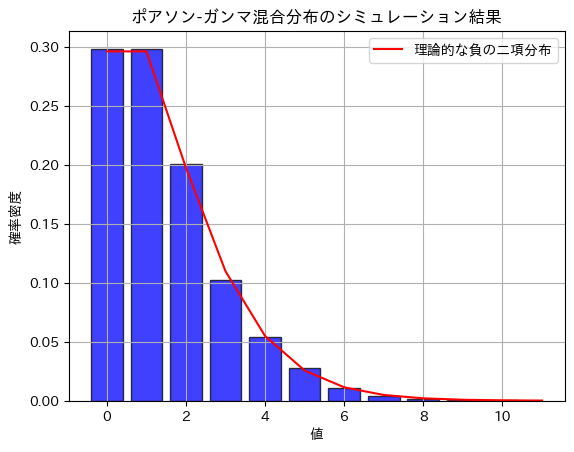
2022 Q3(2)
ガンマ分布の期待値と分散を求めました。
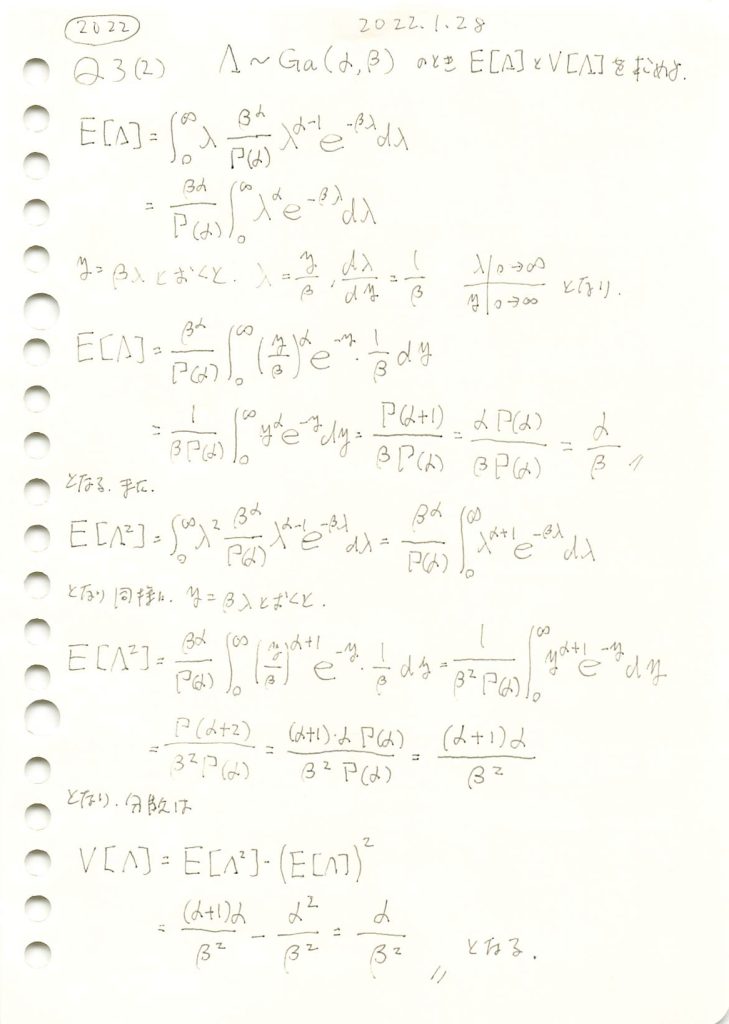
コード
数式を使った計算
## 2022 Q3(2) 2024.8.4
import sympy as sp
# 定義
lambda_var = sp.symbols('lambda')
alpha, beta = sp.symbols('alpha beta', positive=True)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha-1) * sp.exp(-beta * lambda_var)
# 期待値 E[Λ] の計算
expected_value = sp.integrate(lambda_var * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# E[Λ^2] の計算
expected_value_Lambda2 = sp.integrate(lambda_var**2 * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# 分散 V[Λ] の計算
variance = (expected_value_Lambda2 - expected_value**2).simplify()
# 結果を辞書形式で表示
{
"期待値 E[Λ]": expected_value,
"分散 V[Λ]": variance
}{'期待値 E[Λ]': alpha/beta, '分散 V[Λ]': alpha/beta**2}シミュレーションによる計算
## 2022 Q3(2) 2024.8.4
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# サンプルサイズ
sample_size = 10000
# ガンマ分布に従う乱数を生成
samples = np.random.gamma(alpha, 1/beta, sample_size)
# 期待値と分散の計算
expected_value = np.mean(samples)
variance = np.var(samples)
# 結果の表示
print(f"期待値のシミュレーション結果: {expected_value}")
print(f"分散のシミュレーション結果: {variance}")
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なガンマ分布の確率密度関数をプロット
x = np.linspace(0, max(samples), 100)
gamma_pdf = gamma.pdf(x, alpha, scale=1/beta)
plt.plot(x, gamma_pdf, 'r', linestyle='-', label='理論的なガンマ分布')
# グラフのタイトルとラベル
plt.title('ガンマ分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()期待値のシミュレーション結果: 1.4947527551017439
分散のシミュレーション結果: 0.7452822182213243# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# 理論値の計算
theoretical_expected_value = alpha / beta
theoretical_variance = alpha / beta**2
# 結果の表示
print(f"理論値 - 期待値: {theoretical_expected_value}")
print(f"理論値 - 分散: {theoretical_variance}")理論値 - 期待値: 1.5
理論値 - 分散: 0.75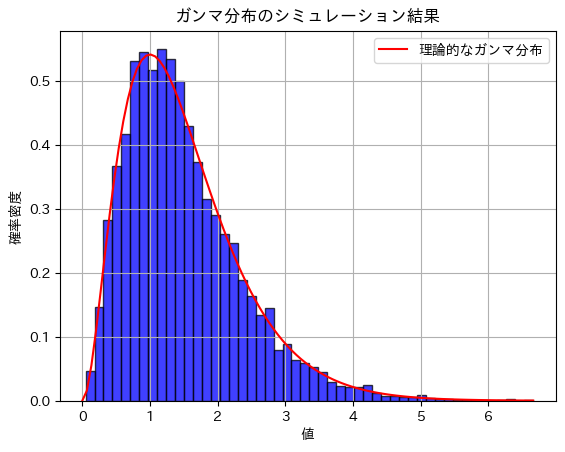
2022 Q3(1)
ポアソン分布の期待値と分散の導出。

コード
数式を使った計算
# 2022 Q3(1) 2024.8.3
import sympy as sp
# 定義
k = sp.symbols('k')
lambda_param = sp.symbols('lambda')
# ポアソン分布の確率関数
poisson_pmf = (lambda_param**k * sp.exp(-lambda_param)) / sp.factorial(k)
# 期待値 E[X] の計算
expected_value = sp.summation(k * poisson_pmf, (k, 0, sp.oo)).simplify()
# E[X^2] の計算
expected_value_X2 = sp.summation(k**2 * poisson_pmf, (k, 0, sp.oo)).simplify()
# 分散 V[X] の計算
variance = (expected_value_X2 - expected_value**2).simplify()
# 結果を表示
{
"期待値 E[X]": expected_value,
"分散 V[X]": variance
}{'期待値 E[X]': lambda, '分散 V[X]': lambda}シミュレーションによる計算
import numpy as np
# パラメータ λ の設定
lambda_param = 5
# シミュレーションの回数
num_simulations = 10000
# 各シミュレーションで生成するサンプルの数
sample_size = 1000
# シミュレーション結果の保存用
expected_values = []
variances = []
for _ in range(num_simulations):
# ポアソン分布に従う乱数を生成
samples = np.random.poisson(lambda_param, sample_size)
# 期待値を計算
expected_values.append(np.mean(samples))
# 分散を計算
variances.append(np.var(samples))
# シミュレーション結果の平均を計算
average_expected_value = np.mean(expected_values)
average_variance = np.mean(variances)
print(f"期待値のシミュレーション結果: {average_expected_value}")
print(f"分散のシミュレーション結果: {average_variance}")
期待値のシミュレーション結果: 4.999602
分散のシミュレーション結果: 4.9992533574プロット
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial
# パラメータ λ の設定
lambda_param = 5
# サンプルサイズ
sample_size = 10000
# ポアソン分布に従う乱数を生成
samples = np.random.poisson(lambda_param, sample_size)
# ヒストグラムの描画
plt.hist(samples, bins=np.arange(0, max(samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なポアソン分布の確率質量関数をプロット
x = np.arange(0, max(samples) + 1)
poisson_pmf = (lambda_param**x * np.exp(-lambda_param)) / factorial(x)
plt.plot(x, poisson_pmf, 'r', marker='o', linestyle='-', label='理論的なポアソン分布')
# グラフのタイトルとラベル
plt.title('ポアソン分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()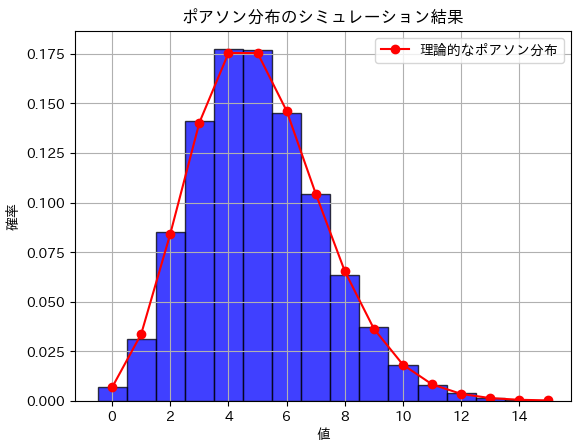
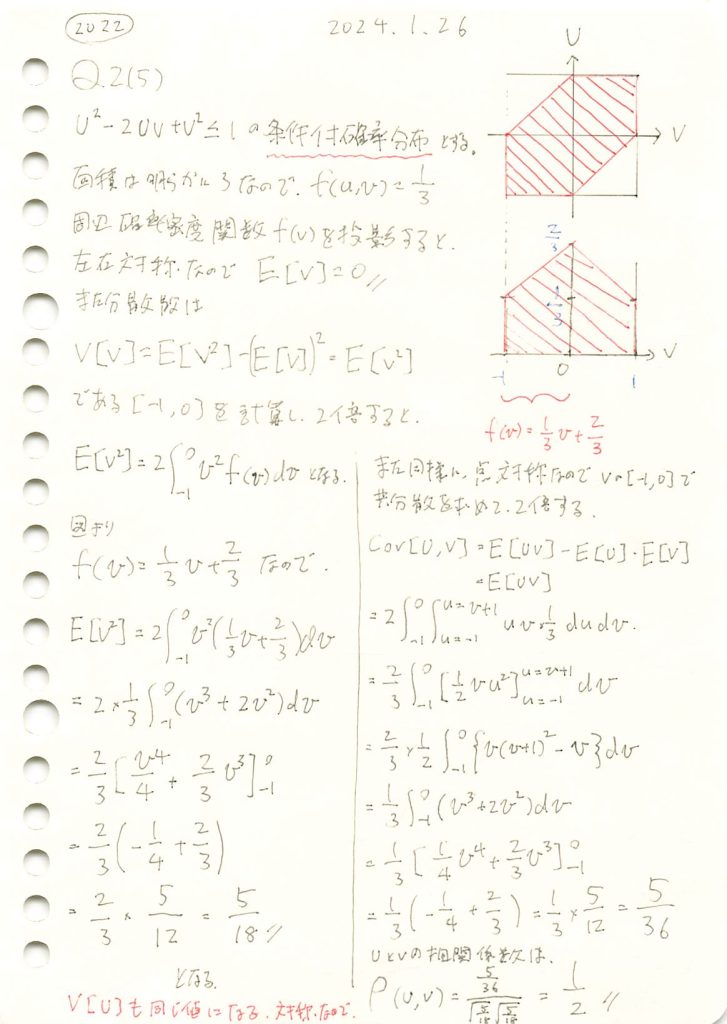
2022 Q2(5)
2変数の条件付き確率を表す図形から相関係数を求める問題をやりました。
コード
二重積分による計算
# 2022 Q2(5) 2024.8.2
import numpy as np
from scipy.integrate import dblquad
# 確率密度関数
def pdf(u, v):
return 1/3 if (u**2 - 2*u*v + v**2 <= 1) else 0
# 期待値 E[U] を計算
E_U, _ = dblquad(lambda v, u: u * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)
# 期待値 E[V] を計算
E_V, _ = dblquad(lambda v, u: v * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)
# 期待値 E[U^2] を計算
E_U2, _ = dblquad(lambda v, u: u**2 * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)
# 期待値 E[V^2] を計算
E_V2, _ = dblquad(lambda v, u: v**2 * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)
# 分散 Var(U) を計算
Var_U = E_U2 - E_U**2
# 分散 Var(V) を計算
Var_V = E_V2 - E_V**2
# 共分散 Cov(U, V) を計算
Cov_UV, _ = dblquad(lambda v, u: u*v * pdf(u, v), -1, 1, lambda u: -1, lambda u: 1)
# 相関係数 ρ(U, V) を計算
rho_UV = Cov_UV / np.sqrt(Var_U * Var_V)
E_U, E_V, Var_U, Var_V, rho_UV
(0.0, 0.0, 0.27777777931630593, 0.2777565638412289, 0.5000186020617616)モンテカルロ法による計算
# 2022 Q2(5) 2024.8.2
import numpy as np
# モンテカルロ法の設定
num_points = 10000
# UとVの一様乱数を生成
U = np.random.uniform(-1, 1, num_points)
V = np.random.uniform(-1, 1, num_points)
# 条件 U^2 - 2UV + V^2 <= 1 を満たす点をフィルタリング
condition = U**2 - 2*U*V + V**2 <= 1
U_filtered = U[condition]
V_filtered = V[condition]
# フィルタリングされた点数
num_filtered_points = len(U_filtered)
# 期待値 E[U] と E[V] の計算
E_U = np.mean(U_filtered)
E_V = np.mean(V_filtered)
# 分散 Var(U) と Var(V) の計算
Var_U = np.var(U_filtered, ddof=1)
Var_V = np.var(V_filtered, ddof=1)
# 共分散 Cov(U, V) の計算
Cov_UV = np.cov(U_filtered, V_filtered, ddof=1)[0, 1]
# 相関係数 ρ(U, V) の計算
rho_UV = Cov_UV / np.sqrt(Var_U * Var_V)
E_U, E_V, Var_U, Var_V, rho_UV, num_filtered_points
(-0.0030089627151707833,
-0.0028658643404494717,
0.2780688116636205,
0.2779098545694732,
0.4835460989080292,
7488)アルゴリズム
モンテカルロ法
- 初期設定
- シミュレーションで使用する点の数を設定する。
- 乱数の生成
- 範囲 [−1,1] でランダムに U と V の値を生成する。
- 条件の適用
- 生成した点の中で、条件
![Rendered by QuickLaTeX.com [ U^2 - 2UV + V^2 \leq 1 ]](https://statistics.blue/wp-content/ql-cache/quicklatex.com-7aa094f6a35fcdeb056477de5d25fe35_l3.png) を満たす点を選び出す。
を満たす点を選び出す。
- 生成した点の中で、条件
- 期待値の計算
- 条件を満たした点の U と V の平均値を計算する。
- 分散の計算
- 条件を満たした点の U と V の分散を計算する。
- 相関係数の計算
- 条件を満たした点の U と V の共分散を計算し、それを用いて相関係数を求める。
- 結果の表示
- 計算した期待値、分散、相関係数、および条件を満たした点の数を表示する。
プロット
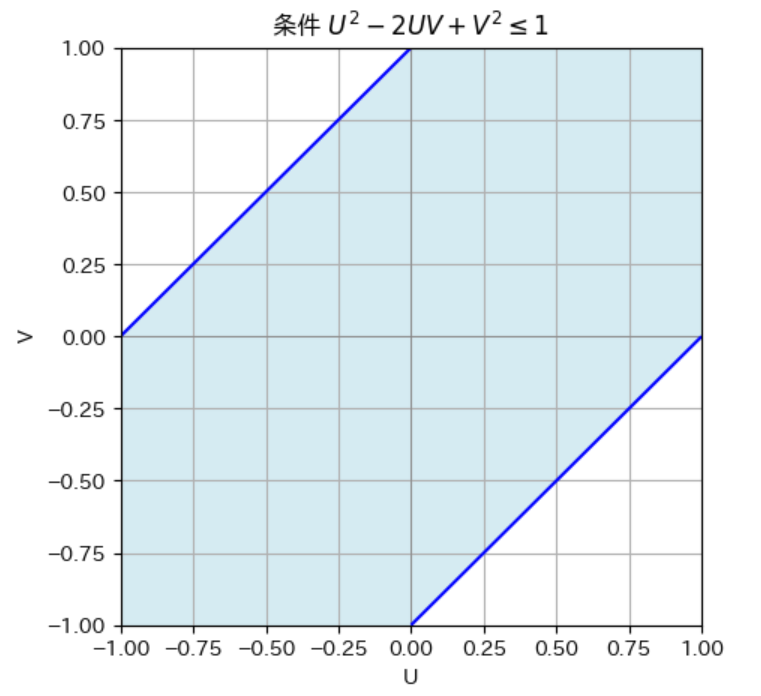
2022 Q2(4)
不等式を図示して面積から確率を求める問題をやりました。

コード
計算
#2022 Q2(4) 2024.8.1
import numpy as np
import scipy.integrate as integrate
# 積分の被積分関数を定義
def integrand(v, u):
return 1/4 if (u**2 - 2*u*v + v**2 <= 1) else 0
# 積分の範囲を定義する関数
def bounds_u():
return -1, 1
def bounds_v(u):
return -1, 1
# 確率 P(U^2 - 2UV + V^2 <= 1) を計算
probability, _ = integrate.nquad(integrand, [bounds_v, bounds_u])
probability
0.7500047152195971プロット
#2022 Q2(4) 2024.8.1
import matplotlib.pyplot as plt
import numpy as np
# UとVの範囲を設定
u = np.linspace(-1, 1, 400)
v = np.linspace(-1, 1, 400)
U, V = np.meshgrid(u, v)
# 条件 U^2 - 2UV + V^2 <= 1 を満たす領域を計算
condition = (U**2 - 2*U*V + V**2 <= 1)
# グラフの描画
plt.figure(figsize=(5, 5))
plt.contourf(U, V, condition, levels=[0.5, 1], colors=['lightblue'], alpha=0.5)
plt.title(r'条件 $U^2 - 2UV + V^2 \leq 1$')
plt.xlabel('U')
plt.ylabel('V')
plt.axhline(0, color='gray', lw=0.5)
plt.axvline(0, color='gray', lw=0.5)
plt.grid(True)
# 条件を満たす境界を描画
plt.contour(U, V, condition, levels=[0.5], colors=['blue'])
plt.show()
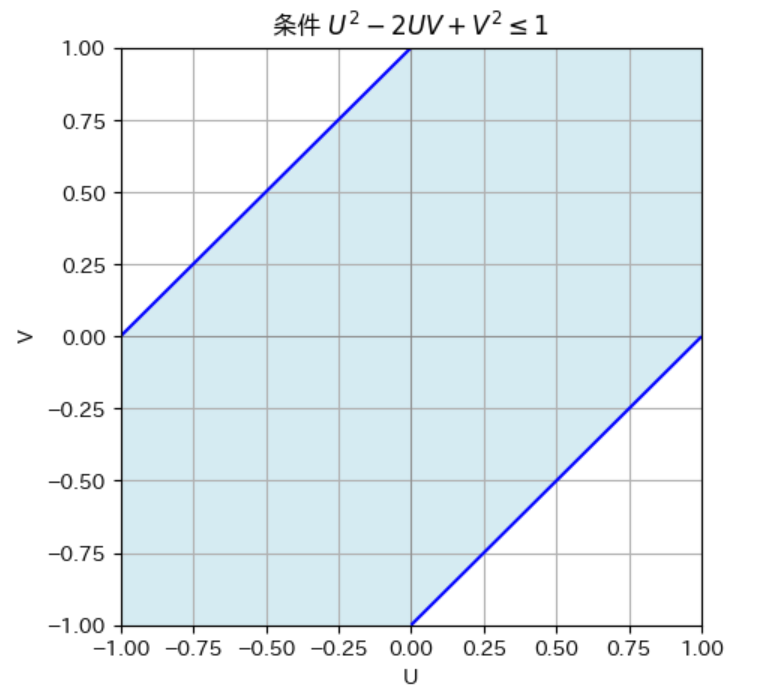
2022 Q2(2)(3)
2変数の独立性の確認と、周辺累積分布関数から周辺確率密度関数を求めました。

コード (2)
#2022 Q2(2) 2024.7.30
from sympy import symbols, integrate
# 変数の定義
u, v = symbols('u v')
# 同時累積分布関数の定義
F_uv = (u*v + u + v + 1) / 4
# 周辺累積分布関数 F1(u) と F2(v) の計算
F1_u = integrate(F_uv, (v, -1, 1))
F2_v = integrate(F_uv, (u, -1, 1))
# 周辺確率密度関数 f1(u) と f2(v) の計算
f1_u = F1_u.diff(u)
f2_v = F2_v.diff(v)
# 同時確率密度関数 f(u,v) を求める
f_uv = F_uv.diff(u).diff(v)
# f(u,v) を f1(u) と f2(v) の積として表す
product_f1_f2 = f1_u * f2_v
# 結果の出力
results = {
'F1_u': F1_u,
'F2_v': F2_v,
'f1_u': f1_u,
'f2_v': f2_v,
'f_uv': f_uv,
'product_f1_f2': product_f1_f2
}
results{'F1_u': u/2 + 1/2,
'F2_v': v/2 + 1/2,
'f1_u': 1/2,
'f2_v': 1/2,
'f_uv': 1/4,
'product_f1_f2': 1/4}コード(3)
計算
#2022 Q2(3) 2024.7.31
from sympy import symbols, pi
import numpy as np
from scipy.integrate import quad
# 符号変数の定義
u, v = symbols('u v')
# f(u,v) の定義
f_uv_value = 1/4
# 条件を満たす範囲でのf(u,v)(数値積分用)
def integrand(v, u):
if u**2 + v**2 <= 1:
return f_uv_value
else:
return 0
# uに関しての積分
def integrate_u(u):
return quad(integrand, -1, 1, args=(u))[0]
# 数値積分による評価
probability_numeric = quad(integrate_u, -1, 1)[0]
# 手計算による値 (π/4) の計算
manual_calculation_value = pi / 4
# 結果の出力
print(f"数値積分による確率: {probability_numeric}\n")
print(f"手計算による値 (π/4): {manual_calculation_value.evalf()}\n")
数値積分による確率: 0.7855319594076084
手計算による値 (π/4): 0.7853981633974483Dプロット
#2022 Q2(3) 2024.7.31
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# u, vの範囲と値を定義
u = np.linspace(-1, 1, 100)
v = np.linspace(-1, 1, 100)
U, V = np.meshgrid(u, v)
# f(u,v)の値を計算
f_uv_value = 1/4
F = np.where(U**2 + V**2 <= 1, f_uv_value, 0)
# 3Dプロットを作成
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(U, V, F, cmap='viridis')
ax.set_xlabel('U')
ax.set_ylabel('V')
ax.set_zlabel('f(u,v)')
ax.set_zlim(0, 1) # z軸の範囲を設定
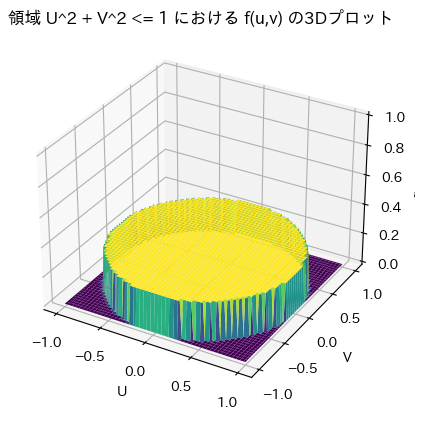
ax.set_title('領域 U^2 + V^2 <= 1 における f(u,v) の3Dプロット')
plt.show()
2022 Q2(1)
同時累積分布関数から周辺累積分布関数と周辺確率密度関数を求める問題をやりました。

コード(解答)
#2022 Q2(1) 2024.7.29
from sympy import symbols, integrate
# 変数の定義
u, v = symbols('u v')
# 同時累積分布関数の定義
F_uv = (u*v + u + v + 1) / 4
# 周辺累積分布関数 F1(u) と F2(v) の計算
F1_u = integrate(F_uv, (v, -1, 1))
F2_v = integrate(F_uv, (u, -1, 1))
F1_u, F2_v
(u/2 + 1/2, v/2 + 1/2)コード(グラフ)
#2022 Q2(1) 2024.7.29
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 同時累積分布関数 F(u, v) を定義
def F(u, v):
return (u * v + u + v + 1) / 4
# u, v の範囲を設定
u = np.linspace(-1, 1, 100)
v = np.linspace(-1, 1, 100)
u, v = np.meshgrid(u, v)
z = F(u, v)
# 3Dプロットの作成
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(u, v, z, cmap='viridis')
# グラフのラベル
ax.set_xlabel('U')
ax.set_ylabel('V')
ax.set_zlabel('F(U, V)')
ax.set_title('同時累積分布関数 F(U, V)')
plt.show()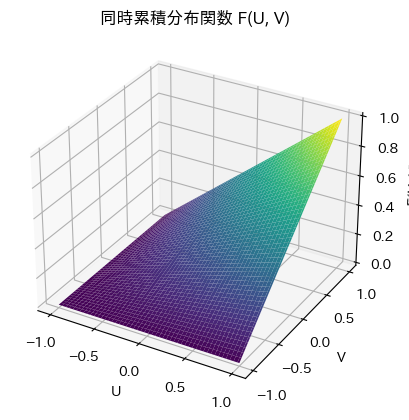
2022 Q1(4)
更に条件が追加された場合のP(A∩B∩C)の取り得る範囲の計算。

コード
#2022 Q1(4) 2024.7.28
# 定数
total_points = 16
PA = 3 / 4
PB = 3 / 4
PC = 3 / 4
PAB = 9 / 16
PAC = 9 / 16
PBC = 9 / 16
# 結果を格納するリスト
valid_probabilities = []
# 最小値と最大値を取るときの組み合わせを格納する変数
min_combination = None
max_combination = None
min_value = float('inf')
max_value = float('-inf')
# 各エリアの点数の範囲を狭める
for n1 in range(total_points // 3 + 1):
for n2 in range((total_points - 3 * n1) // 3 + 1):
for n3 in range(total_points - 3 * n1 - 3 * n2 + 1):
n4 = total_points - 3 * n1 - 3 * n2 - n3
if n4 < 0:
continue
calc_PA = (n1 + 2 * n2 + n4) / total_points
calc_PB = (n1 + 2 * n2 + n4) / total_points
calc_PC = (n1 + 2 * n2 + n4) / total_points
calc_PAB = (n2 + n4) / total_points
calc_PAC = (n2 + n4) / total_points
calc_PBC = (n2 + n4) / total_points
# 条件を満たすか確認
if (abs(calc_PA - PA) < 1e-9 and
abs(calc_PB - PB) < 1e-9 and
abs(calc_PC - PC) < 1e-9 and
abs(calc_PAB - PAB) < 1e-9 and
abs(calc_PAC - PAC) < 1e-9 and
abs(calc_PBC - PBC) < 1e-9):
current_PABC = n4 / total_points
valid_probabilities.append(current_PABC)
if current_PABC < min_value:
min_value = current_PABC
min_combination = (n1, n2, n3, n4)
if current_PABC > max_value:
max_value = current_PABC
max_combination = (n1, n2, n3, n4)
# 最小値と最大値を表示
min_PABC = min_value if valid_probabilities else None
max_PABC = max_value if valid_probabilities else None
# 結果の表示
print(f"最小値: {min_PABC}")
print(f"最大値: {max_PABC}")
print(f"最小値を取るときのN1, N2, N3, N4: {min_combination}")
print(f"最大値を取るときのN1, N2, N3, N4: {max_combination}")
最小値: 0.375
最大値: 0.4375
最小値を取るときのN1, N2, N3, N4: (0, 3, 1, 6)
最大値を取るときのN1, N2, N3, N4: (1, 2, 0, 7)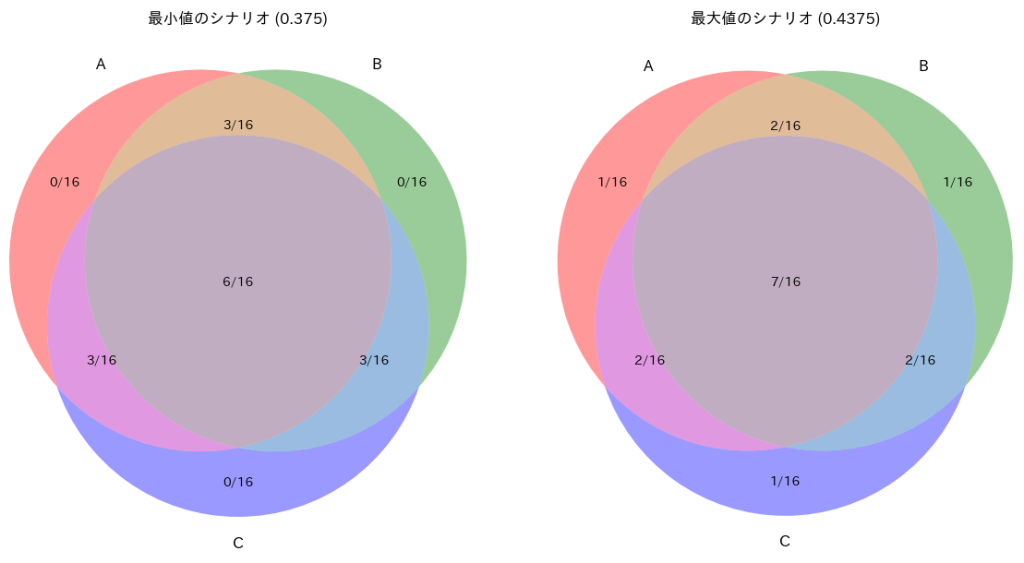
アルゴリズム
1.定数の設定
- 総点数と目標とする確率を設定します。
2.初期化
- 結果を保存するリストと、最小値・最大値、およびそのときの組み合わせを保存する変数を用意します。
3.探索
- 3つのネストされたループを使って、各エリアに割り当てる点数のすべての可能な組み合わせを試します。
- 各組み合わせについて、計算した確率が設定した目標確率と一致するかを確認します。
4.条件を満たす組み合わせの保存
- 条件を満たす場合、その組み合わせをリストに追加します。
- また、その組み合わせが現在の最小値または最大値である場合、それを更新します。
5.結果の表示
- 最小値と最大値、およびそれぞれの組み合わせを表示します。