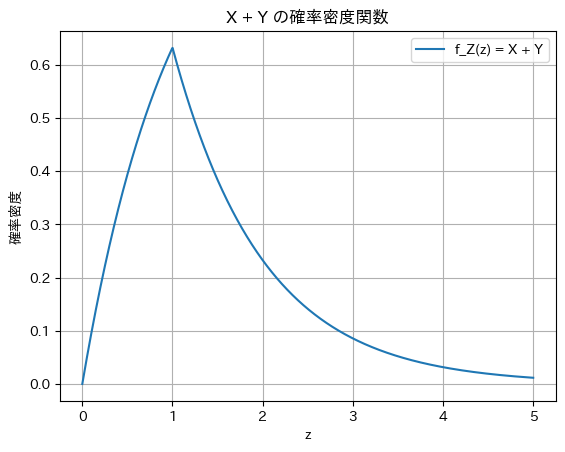
変数変換を用いて二つの分布の和の確率密度関数を求めました。

コード
数式を使った計算
# 2024 Q1(3) 2024.8.19
import sympy as sp
# シンボリック変数の定義
x, z = sp.symbols('x z')
# 確率密度関数の定義
f_X = sp.exp(-x) # f_X(x) = e^(-x)
f_Y = sp.Piecewise((1, (z - x >= 0) & (z - x <= 1)), (0, True)) # f_Y(z - x) for 0 < z - x < 1
# 一般的な積分の設定
f_Z_integral = sp.integrate(f_X * f_Y, (x, 0, z))
# 結果の簡略化
f_Z_general = sp.simplify(f_Z_integral)
# 結果の表示
display(f_Z_general)
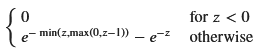
簡単のため、zの範囲を指定して再度計算
# 2024 Q1(3) 2024.8.19
import sympy as sp
# シンボリック変数の定義
x, z = sp.symbols('x z')
# 確率密度関数の定義
f_X = sp.exp(-x) # f_X(x) = e^(-x)
f_Y = 1 # f_Y(y) = 1 (0 < y < 1)
# 各範囲での計算
# 1. z <= 0 の場合
f_Z_1 = 0 # z <= 0 の場合は f_Z(z) = 0
# 2. 0 < z <= 1 の場合
f_Z_2_integral = sp.integrate(f_X * f_Y, (x, 0, z))
f_Z_2 = sp.simplify(f_Z_2_integral)
# 3. z > 1 の場合
f_Z_3_integral = sp.integrate(f_X * f_Y, (x, z-1, z))
f_Z_3 = sp.simplify(f_Z_3_integral)
# 結果の表示
print(f"f_Z(z) for z <= 0:")
display(f_Z_1)
print(f"f_Z(z) for 0 < z <= 1:")
display(f_Z_2)
print(f"f_Z(z) for z > 1:")
display(f_Z_3)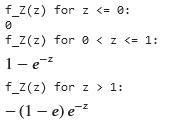
プロット
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
# 確率密度関数 f_X(x) と f_Y(y)
def f_X(x):
return np.exp(-x) if x > 0 else 0
def f_Y(y):
return 1 if 0 < y < 1 else 0
# Z = X + Y の確率密度関数 f_Z(z) の計算
def f_Z(z):
integrand = lambda x: f_X(x) * f_Y(z - x)
return quad(integrand, max(0, z-1), z)[0] #積分範囲を限定する場合
#return quad(integrand, 0, z, epsabs=1e-8, epsrel=1e-8)[0] #積分範囲を広くする場合
# z の範囲を設定し、f_Z(z) を計算
z_values = np.linspace(0, 5, 1000) # 増加させたサンプル数
f_Z_values = np.array([f_Z(z) for z in z_values])
# グラフの描画
plt.plot(z_values, f_Z_values, label='f_Z(z) = X + Y')
plt.xlabel('z')
plt.ylabel('確率密度')
plt.title('X + Y の確率密度関数')
plt.legend()
plt.grid(True)
plt.show()