対数尤度関数を用いてパラメータの最尤推定量を求めました。

コード
数式を使った計算
# 2022 Q4(3) 2024.8.10
import sympy as sp
# シンボリック変数の定義
gamma = sp.Symbol('gamma', positive=True)
n = 10 # 具体的なサンプル数を設定
X = sp.symbols('X1:%d' % (n+1), positive=True) # X1, X2, ..., Xn を定義
# 尤度関数の定義
L_gamma = sp.prod((1/gamma) * X[i]**(-(1/gamma + 1)) for i in range(n))
# 対数尤度関数の定義
log_L_gamma = sp.log(L_gamma)
# 對数尤度関数を γ で微分
diff_log_L_gamma = sp.diff(log_L_gamma, gamma)
# 微分した結果を 0 に等しいとおいて解く
gamma_hat_eq = sp.Eq(diff_log_L_gamma, 0)
gamma_hat = sp.solve(gamma_hat_eq, gamma)
# 結果の表示
sp.pprint(gamma_hat[0], use_unicode=True)
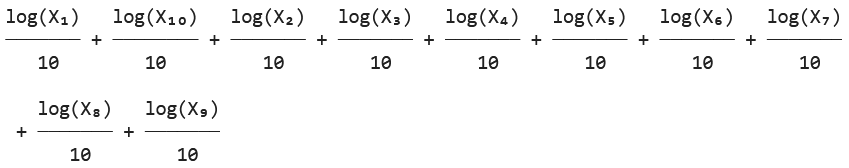
シミュレーションによる計算
# 2022 Q4(3) 2024.8.10
import numpy as np
# 観測データ(例としてランダムに生成)
n = 1000 # データ点の数
gamma_true = 0.5 # 実際の γ (例として)
# CDFの逆関数
X = (np.random.uniform(size=n))**(-gamma_true)
# 最尤推定量 gamma_hat} の計算
log_X = np.log(X)
gamma_hat = np.mean(log_X)
print(f"観測(ランダム)データからの最尤推定量 gamma_hat: {gamma_hat}")観測(ランダム)データからの最尤推定量 gamma_hat: 0.4984974482026361