事象A,B,Cが独立とは限らない場合のP(A∩B∩C)の取り得る範囲を求めました。

コード
### 2022 Q1(3) 2024.7.27
import itertools
def generate_combinations(n, k):
base_list = [1] * k + [0] * (n - k)
all_combinations = set(itertools.permutations(base_list))
return list(all_combinations)
def calculate_intersection(A, B, C):
return np.mean(np.array(A) & np.array(B) & np.array(C))
def find_min_max_intersection(n, k):
all_combinations = generate_combinations(n, k)
min_intersection = 1.0
max_intersection = 0.0
for A in all_combinations:
for B in all_combinations:
for C in all_combinations:
intersection_ratio = calculate_intersection(A, B, C)
if intersection_ratio < min_intersection:
min_intersection = intersection_ratio
if intersection_ratio > max_intersection:
max_intersection = intersection_ratio
return min_intersection, max_intersection
# パラメータを設定
n = 8
k = 6
# 最小値と最大値を計算
min_intersection, max_intersection = find_min_max_intersection(n, k)
min_intersection, max_intersection
(0.25, 0.75)アルゴリズム
- 組み合わせの生成
- 配列の長さ
nを8、1の数kを6と設定する。 - 配列
11111100を作成し、itertools.permutationsを使ってすべての並べ替えを生成する。
- 配列の長さ
- 交差部分の確率計算
- すべての組み合わせに対して、配列
A,B,Cを選ぶ。 - 例えば、
A = 11111100,B = 11011110,C = 11101110の場合、交差部分A & B & Cは11001100となる。これにより、確率は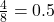 となる。
となる。
- すべての組み合わせに対して、配列
- 最小値と最大値の取得
- すべての組み合わせに対して計算した確率を比較し、最小値と最大値を更新する。
- 最終的に、最小値と最大値を返す。