線形変換された確率変数ベクトルの分散共分散行列を求める問題をやりました。
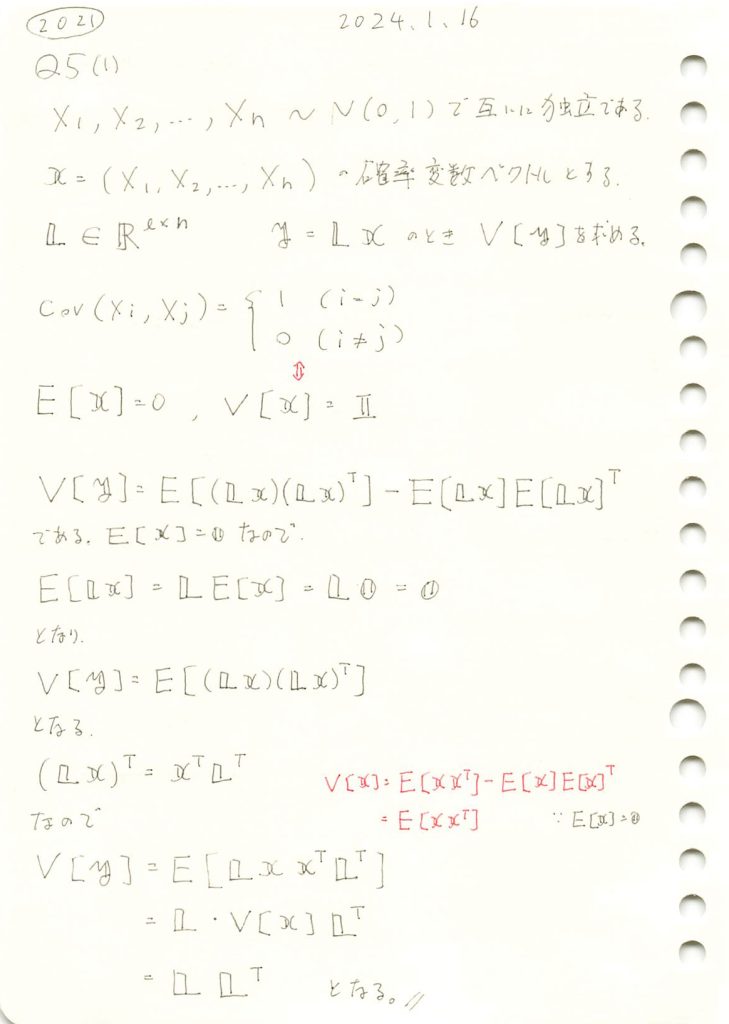
コード
シミュレーション
乱数による分散共分散行列と、![]() を比較します
を比較します
# 2021 Q5(1) 2024.9.4
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 標準正規分布からサンプルを生成
n = 1000 # サンプル数
d = 5 # 次元数
X = np.random.randn(d, n)
# 4x5の線形変換行列 L を定義
L = np.array([[9, 7, 8, 6, 5],
[6, 5, 4, 3, 2],
[3, 2, 1, 9, 8],
[8, 7, 6, 5, 0]])
# 線形変換を適用して y を計算
Y = np.dot(L, X)
# y のサンプルから分散共分散行列を推定
V_Y_estimated = np.cov(Y)
# 理論的な L・L^T と比較
V_Y_theoretical = np.dot(L, L.T)
# ヒートマップのプロット
plt.figure(figsize=(12, 6))
# 推定された分散共分散行列のヒートマップ
plt.subplot(1, 2, 1)
sns.heatmap(V_Y_estimated, annot=True, cmap="coolwarm", cbar=True)
plt.title("推定された分散共分散行列")
# 理論的な分散共分散行列のヒートマップ
plt.subplot(1, 2, 2)
sns.heatmap(V_Y_theoretical, annot=True, cmap="coolwarm", cbar=True)
plt.title("理論的な分散共分散行列")
plt.show()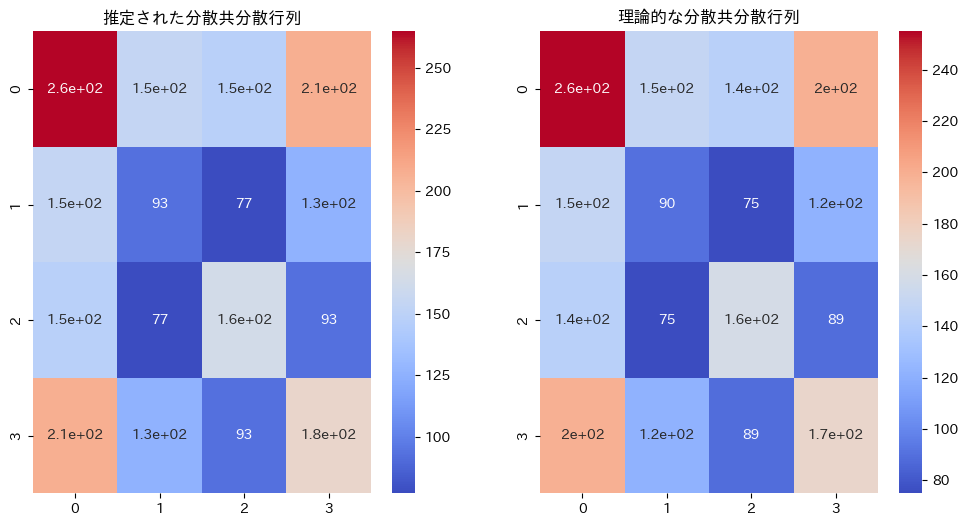
同じような行列になりました。違いは乱数によるものです。