τハットがτの不偏推定量になるための必要十分条件を求める問題を学びました。
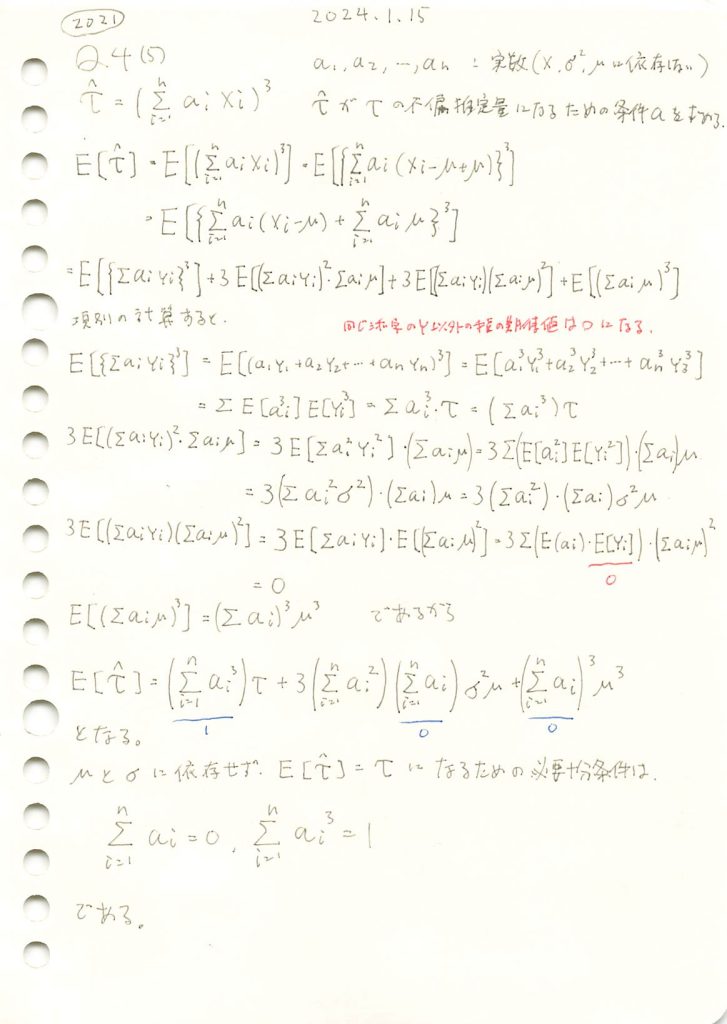
コード
![]() を満たすaiを見つける
を満たすaiを見つける
# 2021 Q4(5) 2024.9.3
import numpy as np
def find_ai_sequence(n, tolerance=1e-6):
while True:
# ランダムに n 個の値を生成
a = np.random.uniform(-1, 1, n)
# 正の数と負の数の個数を調整
neg_count = (n + 1) // 2 # 負の数を1つ多くする
pos_count = n - neg_count
a[:pos_count] = np.abs(a[:pos_count])
a[pos_count:] = -np.abs(a[pos_count:])
# 合計が0になるように調整
a -= np.mean(a)
# 条件をチェック
sum_ai = np.sum(a)
sum_ai_cubed = np.sum(a**3)
if np.abs(sum_ai) < tolerance and np.abs(sum_ai_cubed - 1) < tolerance:
return a
# パラメータの設定
n = 10 # サンプル数
# 条件を満たす a_i の数列を見つける
a = find_ai_sequence(n)
# 計算を確認
print(f"a_i の合計 (≒0): {a.sum()}")
print(f"a_i^3 の合計 (≒1): {np.sum(a ** 3)}")
# 条件を満たした a_i を表示
print("a_i の数列:")
print(a)a_i の合計 (≒0): 6.661338147750939e-16
a_i^3 の合計 (≒1): 1.0000001485058854
a_i の数列:
[ 0.13279542 1.05885499 0.24951311 0.83492921 0.13800083 -0.71178855
-0.38213634 -0.18394766 -0.55820111 -0.5780199 ]5分ほどで見つかった
見つかったaiと指数分布に従う乱数を使って![]() のシミュレーションしてみる
のシミュレーションしてみる
import numpy as np
import matplotlib.pyplot as plt
# すでに見つかった条件を満たす a_i を使用
a = np.array([ 0.13279542, 1.05885499, 0.24951311, 0.83492921, 0.13800083, -0.71178855,
-0.38213634, -0.18394766, -0.55820111, -0.5780199 ])
# パラメータの設定
n = len(a) # サンプル数(a_i の数と一致させる)
scale = 1.0 # 指数分布のスケールパラメータ
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
tau_hat_values = []
# シミュレーションを実行
for _ in range(iterations):
# 指数分布に従う乱数を生成
X = np.random.exponential(scale=scale, size=n)
# \hat{\tau} の計算
tau_hat = np.sum(a * X) ** 3
tau_hat_values.append(tau_hat)
# 指数分布の三次中心モーメントを計算
tau = 2 * scale**3 # 指数分布における三次中心モーメント
# シミュレーション結果の平均
simulated_mean_tau_hat = np.mean(tau_hat_values)
# 結果を表示
print(f"理論値の τ: {tau}")
print(f"シミュレーションによる τ の推定値: {simulated_mean_tau_hat}")
# 視覚化
plt.figure(figsize=(10, 6))
plt.hist(tau_hat_values, bins=50, alpha=0.75, label='シミュレーション結果')
plt.axvline(simulated_mean_tau_hat, color='red', linestyle='dashed', linewidth=2, label=f'シミュレーション平均 = {simulated_mean_tau_hat:.2f}')
plt.axvline(tau, color='blue', linestyle='dashed', linewidth=2, label=f'理論値 = {tau:.2f}')
plt.xlabel('値')
plt.ylabel('頻度')
plt.title(r"$\hat{\tau} = \left(\sum_{i=1}^{n} a_i X_i\right)^3$ の分布 (指数分布)")
plt.legend()
plt.grid(True)
plt.show()理論値の τ: 2.0
シミュレーションによる τ の推定値: 2.0555706049874143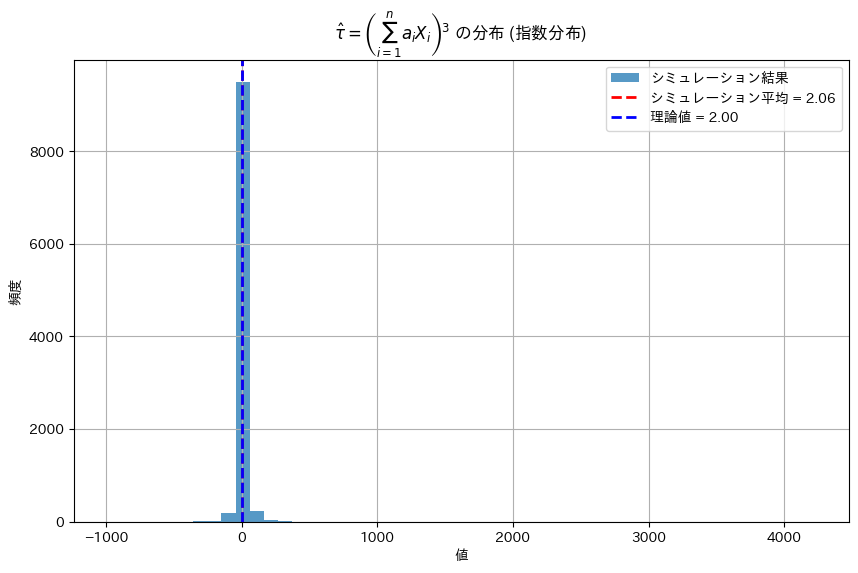
推定値は理論値と近い値をとった。ただし1.5~2.5付近で値が変動する。原因として、n=10が小さい、三次であるから乱数のばらつきに敏感、指数分布は大きな値をとる、が挙げられる。