標本平均との差の3乗の和の期待値を求める問題をやりました。
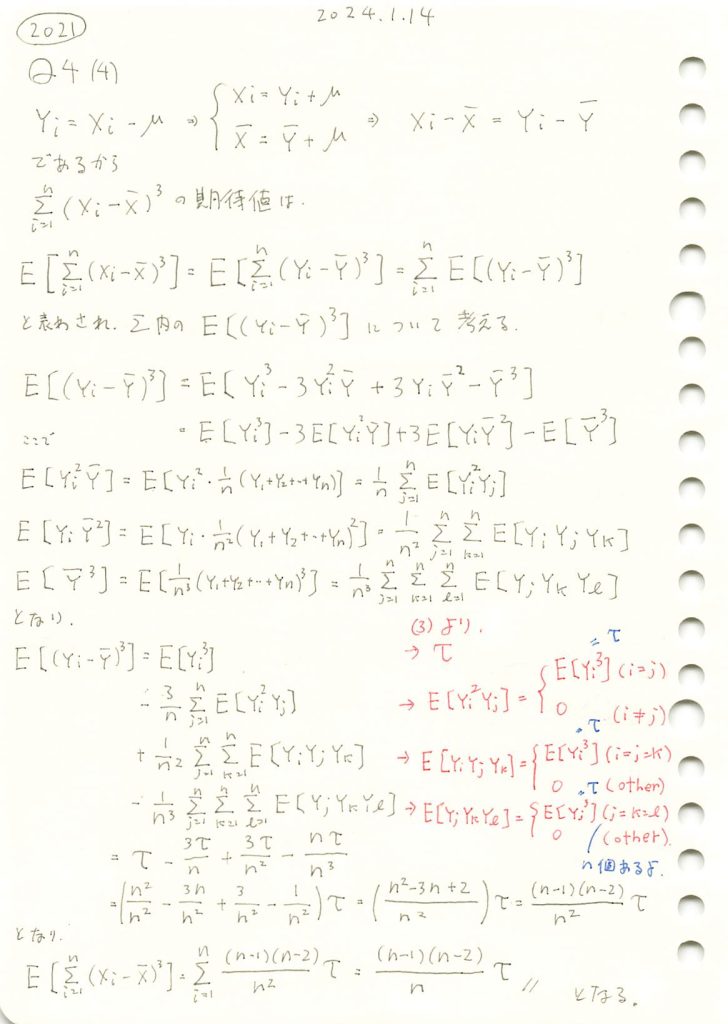
コード
シミュレーションをして理論値と比較します
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 10 # サンプル数 (必要に応じて変更可能)
scale = 1.0 # 指数分布のスケールパラメータ(1/λ)
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
sum_X_i_minus_X_bar_cubed_values = []
# シミュレーションを実行
for _ in range(iterations):
# 指数分布に従う乱数を生成
X = np.random.exponential(scale=scale, size=n)
# 標本平均を計算
X_bar = np.mean(X)
# (X_i - X_bar)^3 の合計を計算
sum_X_i_minus_X_bar_cubed = np.sum((X - X_bar)**3)
sum_X_i_minus_X_bar_cubed_values.append(sum_X_i_minus_X_bar_cubed)
# 指数分布の三次中心モーメントを計算
tau = 2 * scale**3 # 指数分布における三次中心モーメント
# 理論値の計算
theoretical_value = (n - 1) * (n - 2) * tau / n
# シミュレーション結果の平均
simulated_mean = np.mean(sum_X_i_minus_X_bar_cubed_values)
# 結果を表示
print(f"理論値: {theoretical_value}")
print(f"シミュレーションによる平均: {simulated_mean}")
# 視覚化
plt.figure(figsize=(10, 6))
plt.hist(sum_X_i_minus_X_bar_cubed_values, bins=50, alpha=0.75, label='シミュレーション結果')
plt.axvline(simulated_mean, color='red', linestyle='dashed', linewidth=2, label=f'シミュレーション平均 = {simulated_mean:.2f}')
plt.axvline(theoretical_value, color='blue', linestyle='dashed', linewidth=2, label=f'理論値 = {theoretical_value:.2f}')
plt.xlabel('値')
plt.ylabel('頻度')
plt.title(r"$\sum_{i=1}^{n} (X_i - \overline{X})^3$ の分布 (指数分布)")
plt.legend()
plt.grid(True)
plt.show()理論値: 14.4
シミュレーションによる平均: 14.499748799877718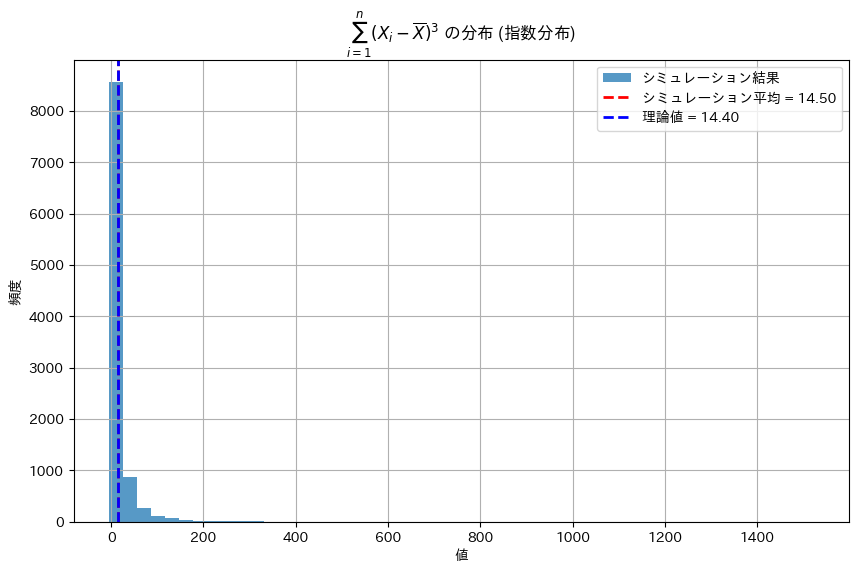
シミュレーションは理論値に近い値を示しました
コード中の三次中心モーメントの導出を下記に示します
指数分布の三次中心モーメント (=τ) の導出
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()