ポアソン分布に従う複数の確率変数の和が正規分布に近似するとした場合の信頼区間を求める問題を学びました。
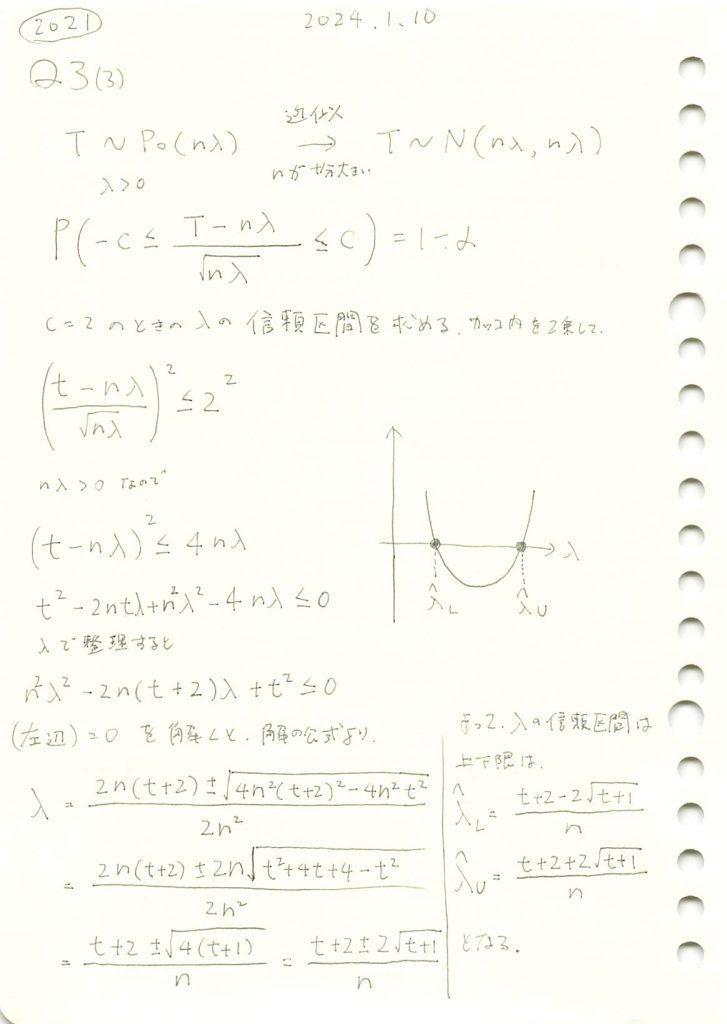
コード
二次方程式を解いて信頼区間を求めます
# 2021 Q3(3) 2024.8.29
import sympy as sp
# 変数の定義
n, lambda_, T = sp.symbols('n lambda_ T', real=True, positive=True)
c = 2
# 不等式を通常の方程式として変換
# まず、二次方程式の形を導出
lhs = sp.Eq((T - n*lambda_)**2, (c**2) * n * lambda_)
# λに関する二次方程式を解く
solutions = sp.solve(lhs, lambda_)
# 解の表示
lambda_L = solutions[0].simplify()
lambda_U = solutions[1].simplify()
# 結果の表示
display(lambda_L, lambda_U)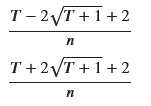
シミュレーションで、真のλが信頼区間に含まれる割合を求めます
# 2021 Q3(3) 2024.8.29
import numpy as np
# パラメータの設定
lambda_true = 5 # 真の λ の値
n = 10 # サンプル数
num_simulations = 1000 # シミュレーションの回数
# 結果を保存するカウンター
within_confidence = 0
# シミュレーション開始
for _ in range(num_simulations):
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_true, n)
T = np.sum(samples) # T を計算
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
# 真のλが信頼区間内にあるか確認
if lambda_L <= lambda_true <= lambda_U:
within_confidence += 1
# 信頼区間内に真のλが含まれる割合を計算
coverage = within_confidence / num_simulations
# 結果の表示
print(f"{num_simulations}回のシミュレーションのうち、真のλが信頼区間内に含まれていた割合: {coverage:.4f}")1000回のシミュレーションのうち、真のλが信頼区間内に含まれていた割合: 0.9550c=2のとき信頼区間の信頼率は95.45%となり、シミュレーションと概ね一致します
上のシミュレーションを視覚化します
# 2021 Q3(3) 2024.8.29
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
lambda_true = 5 # 真の λ の値
n = 10 # サンプル数
num_simulations = 1000 # シミュレーションの回数
# 結果を保存するリスト
lower_limits = []
upper_limits = []
within_confidence = 0
# シミュレーション開始
for _ in range(num_simulations):
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_true, n)
T = np.sum(samples) # T を計算
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
# 信頼区間の記録
lower_limits.append(lambda_L)
upper_limits.append(lambda_U)
# 真のλが信頼区間内にあるか確認
if lambda_L <= lambda_true <= lambda_U:
within_confidence += 1
# 信頼区間内に真のλが含まれる割合を計算
coverage = within_confidence / num_simulations
print(f"{num_simulations}回のシミュレーションのうち、真のλが信頼区間内に含まれていた割合: {coverage:.4f}")
# ヒストグラムのプロット
plt.figure(figsize=(12, 6))
plt.hist(lower_limits, bins=30, alpha=0.5, label='信頼区間の下限', color='blue')
plt.hist(upper_limits, bins=30, alpha=0.5, label='信頼区間の上限', color='red')
plt.axvline(lambda_true, color='green', linestyle='--', label='真の λ')
plt.title('信頼区間の分布')
plt.xlabel('λ の値')
plt.ylabel('頻度')
plt.legend()
plt.grid(True)
plt.show()
# 信頼区間のプロット
plt.figure(figsize=(12, 6))
for i in range(num_simulations):
plt.plot([lower_limits[i], upper_limits[i]], [i, i], color='blue')
plt.axvline(lambda_true, color='red', linestyle='--', label='真の λ')
plt.title('シミュレーションごとの信頼区間')
plt.xlabel('λ の値')
plt.ylabel('シミュレーション回数')
plt.legend()
plt.grid(True)
plt.show()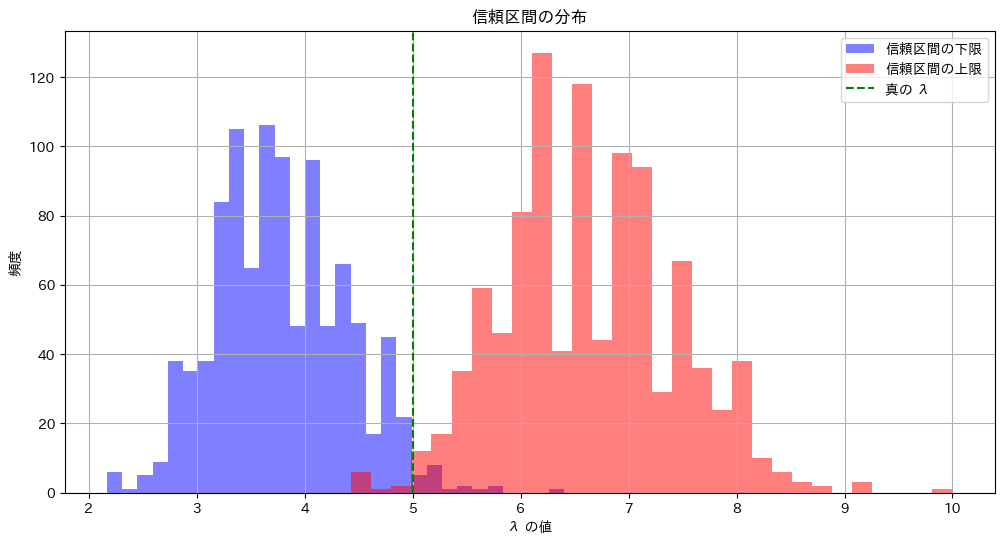
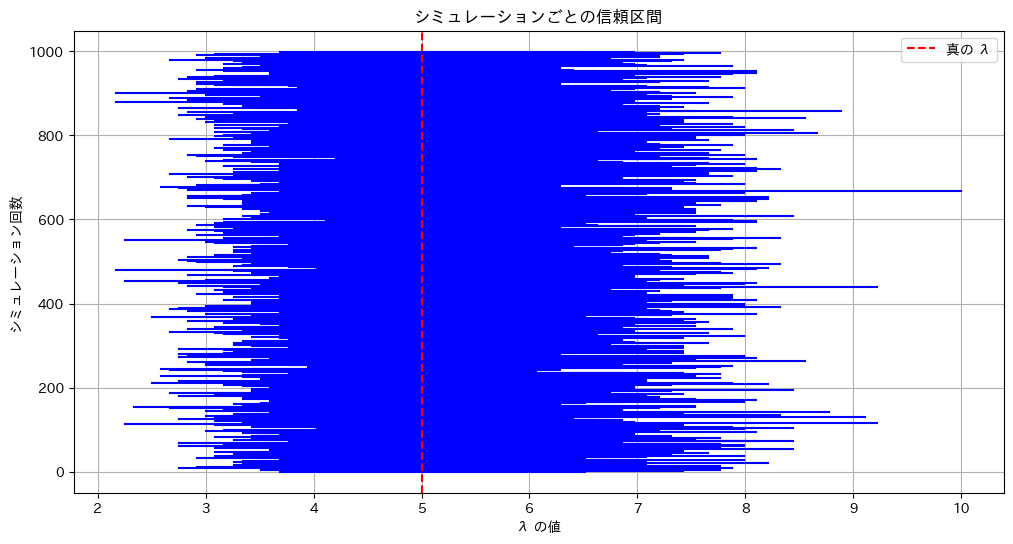
真のλが95.45%の確率で信頼区間内に含まれている様子が確認できました。