ポアソン分布に従う確率変数の和Tからλの最尤推定量を求める問題をやりました。
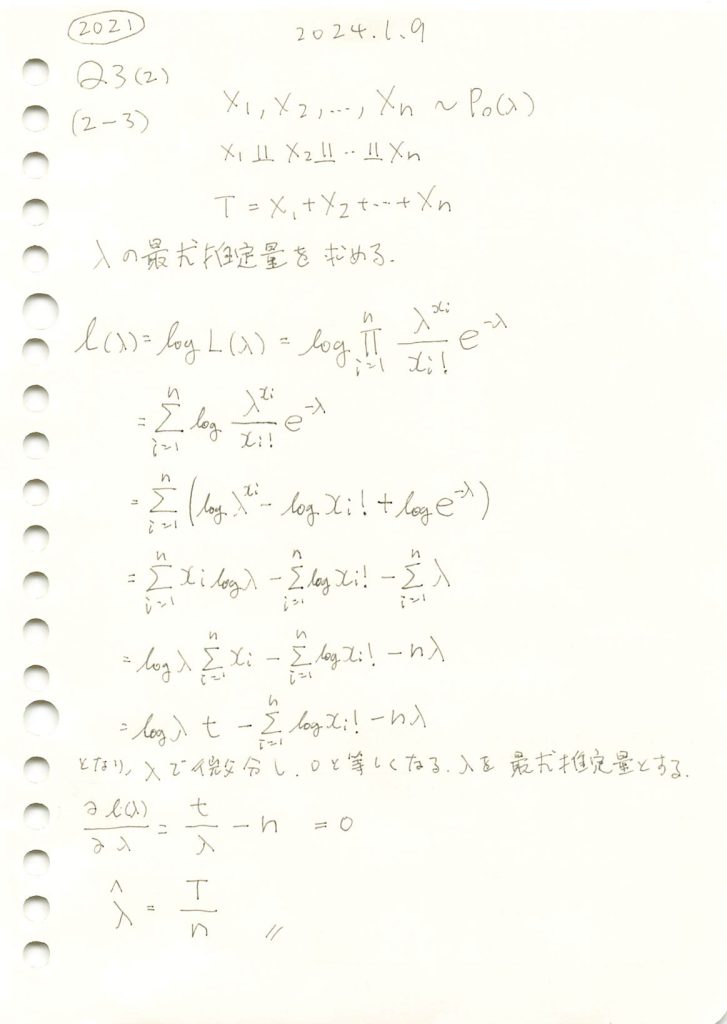
あとがき
![]() の式で計算すると簡単。
の式で計算すると簡単。
コード
scipyのminimizeで、最尤推定量を探索する。
# 2021 Q3(2)[2-3] 2024.8.28
import numpy as np
from scipy.optimize import minimize
from scipy.stats import poisson
# パラメータの設定
lambda_value = 5 # 真のパラメータ(実際のλ)
n = 10 # サンプル数
num_simulations = 1000 # シミュレーション回数
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, n)
# 尤度関数(負の対数尤度関数)
def negative_log_likelihood(lambda_hat, data):
# ポアソン分布に基づく対数尤度を計算。minimizeを用いるためマイナス符号をつける
return -np.sum(poisson.logpmf(data, lambda_hat))
# 最尤推定量の推定
initial_guess = np.mean(samples) # 初期値としてサンプルの平均を使用
result = minimize(negative_log_likelihood, x0=initial_guess, args=(samples,), bounds=[(0.001, None)])
lambda_mle = result.x[0]
# 結果を表示
print(f"実際のλ: {lambda_value}")
print(f"推定されたλの最尤推定値: {lambda_mle}")実際のλ: 5
推定されたλの最尤推定値: 4.9尤度関数のグラフを確認
# 2021 Q3(2)[2-3] 2024.8.28
import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt
# パラメータの設定
lambda_value = 5 # 真のパラメータ(実際のλ)
n = 10 # サンプル数
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, n)
# 尤度関数を定義
def likelihood(lambda_hat, data):
return np.prod(poisson.pmf(data, lambda_hat))
# 尤度関数と対数尤度関数の計算
lambda_range = np.linspace(0.1, 10, 500) # すべてのグラフで共通の範囲
likelihood_values = [likelihood(l, samples) for l in lambda_range]
log_likelihood_values = np.log(likelihood_values)
# 最大の尤度を与えるλを求める
max_likelihood_lambda = lambda_range[np.argmax(likelihood_values)]
# グラフのプロット
fig, ax = plt.subplots(2, 1, figsize=(10, 6))
# 尤度関数のプロット
ax[0].plot(lambda_range, likelihood_values, label='尤度', color='blue')
ax[0].axvline(x=max_likelihood_lambda, color='red', linestyle='--', label=f'最大尤度 λ = {max_likelihood_lambda:.2f}')
ax[0].set_title("尤度関数")
ax[0].set_xlabel("λ の値")
ax[0].set_ylabel("尤度")
ax[0].set_xlim(lambda_range[0], lambda_range[-1]) # 横軸を合わせる
ax[0].legend()
ax[0].grid(True)
# 対数尤度関数のプロット
ax[1].plot(lambda_range, log_likelihood_values, label='対数尤度', color='green')
ax[1].axvline(x=max_likelihood_lambda, color='red', linestyle='--', label=f'最大尤度 λ = {max_likelihood_lambda:.2f}')
ax[1].set_title("対数尤度関数")
ax[1].set_xlabel("λ の値")
ax[1].set_ylabel("対数尤度")
ax[1].set_xlim(lambda_range[0], lambda_range[-1]) # 横軸を合わせる
ax[1].legend()
ax[1].grid(True)
# グラフの表示
plt.tight_layout()
plt.show()
# 最終結果の表示
print(f"実際のλ: {lambda_value}")
print(f"推定されたλの最尤推定値: {max_likelihood_lambda}")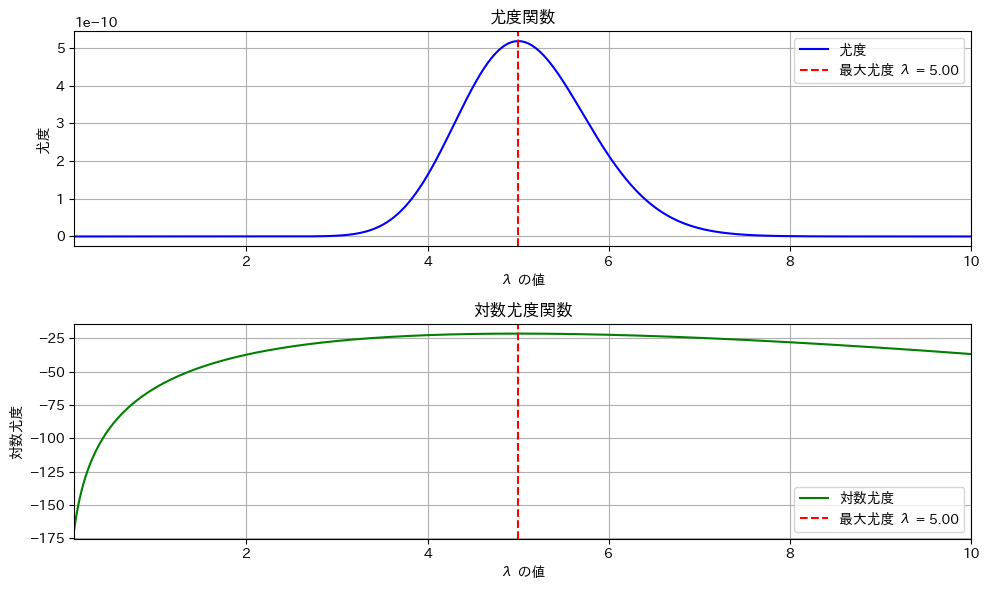
尤度関数でも対数尤度関数でも同じλでピークになる。
nが小さいとλの推定量の分散が大きくなるので誤差が大きくなる。上のグラフはたまたま5.00になった。n=100ぐらいにすると安定する。
シミュレーションによる計算
# 2021 Q3(2)[2-3] 2024.8.28
import numpy as np
# パラメータの設定
lambda_value = 5 # 真のパラメータ(実際のλ)
n = 10 # サンプル数
num_simulations = 1000 # シミュレーション回数
# ポアソン分布に従う n 個のサンプルを num_simulations 回生成
samples = np.random.poisson(lambda_value, (num_simulations, n))
# 各サンプルの和 T を計算
T = np.sum(samples, axis=1)
# λ の最尤推定量を計算
lambda_hat = T / n
# 結果を表示
print(f"実際のλ: {lambda_value}")
print(f"推定されたλの平均: {np.mean(lambda_hat)}")
print(f"推定されたλの分散: {np.var(lambda_hat)}")実際のλ: 5
推定されたλの平均: 5.0058
推定されたλの分散: 0.49292636