ホーム » コードあり » 2021 Q3(1)

2021 Q3(1)

投稿者: in コードあり, ポアソン分布, 統計検定1級 2021年 統計数理 投稿日: 最終更新日:

ポアソン分布のモーメント母関数を求めました。

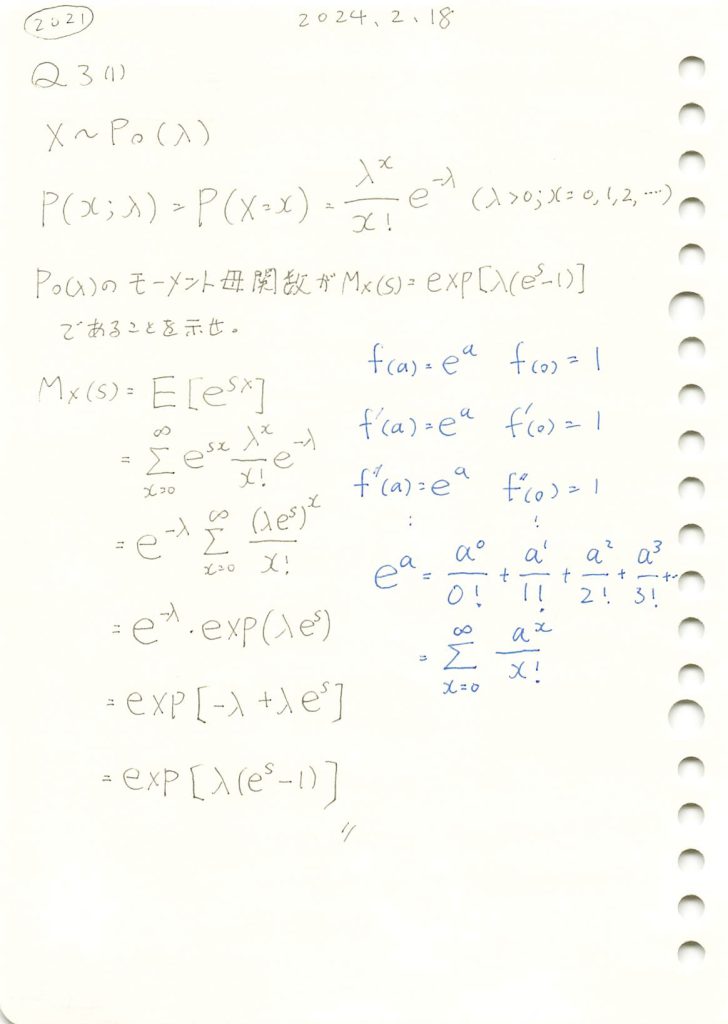
コード

数式を使った計算

# 2021 Q3(1)  2024.8.25

import sympy as sp

# 変数の定義
s, x, lambda_ = sp.symbols('s x lambda_', real=True, positive=True)

# ポアソン分布の確率質量関数 (PMF)
poisson_pmf = (lambda_**x * sp.exp(-lambda_)) / sp.factorial(x)

# モーメント母関数 M_X(s) の定義
M_X = sp.summation(sp.exp(s*x) * poisson_pmf, (x, 0, sp.oo))

# 結果を簡略化
M_X_simplified = sp.simplify(M_X)

# 結果を表示
M_X_simplified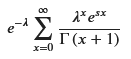

無限級数がe^xの形に変換されないようです。

exp(s) を t に置き換えて、最後に戻してみます。

# 2021 Q3(1)  2024.8.25

import sympy as sp

# 変数の定義
s, x, lambda_, t = sp.symbols('s x lambda_ t', real=True, positive=True)

# exp(s) を t に置き換え
summand = (lambda_ * t)**x / sp.factorial(x)

# モーメント母関数 M_X(s) の定義
M_X = sp.exp(-lambda_) * sp.summation(summand, (x, 0, sp.oo))

# 簡略化
M_X_simplified = sp.simplify(M_X)

# 最後に t を exp(s) に戻す
M_X_final = M_X_simplified.subs(t, sp.exp(s))

# 結果を表示
M_X_final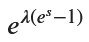

手計算と同じ形になりました。

モーメント母関数を使って期待値と分散を求めます。

import sympy as sp

# 変数の定義
s, lambda_ = sp.symbols('s lambda_', real=True, positive=True)

# モーメント母関数 M_X(s) の定義
M_X = sp.exp(lambda_ * (sp.exp(s) - 1))

# 1次モーメント（期待値）の計算
M_X_prime = sp.diff(M_X, s)
expectation = M_X_prime.subs(s, 0)

# 2次モーメントの計算
M_X_double_prime = sp.diff(M_X_prime, s)
second_moment = M_X_double_prime.subs(s, 0)

# 分散の計算
variance = second_moment - expectation**2

# 結果を表示
display(expectation, variance)