離散型確率分布の正規化定数を計算しました。

コード
数式を使った計算
# 2021 Q2(3) 2024.8.23
from sympy import symbols, summation, Eq, solve
# 記号の定義
n = symbols('n', integer=True)
C = symbols('C', real=True)
# 和を計算
sum_expr = summation(C * (n + 1), (n, 0, 100))
# 正規化条件を設定
normalization_condition = Eq(sum_expr, 1)
# C を解く
C_value = solve(normalization_condition, C)[0]
C_value
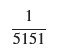
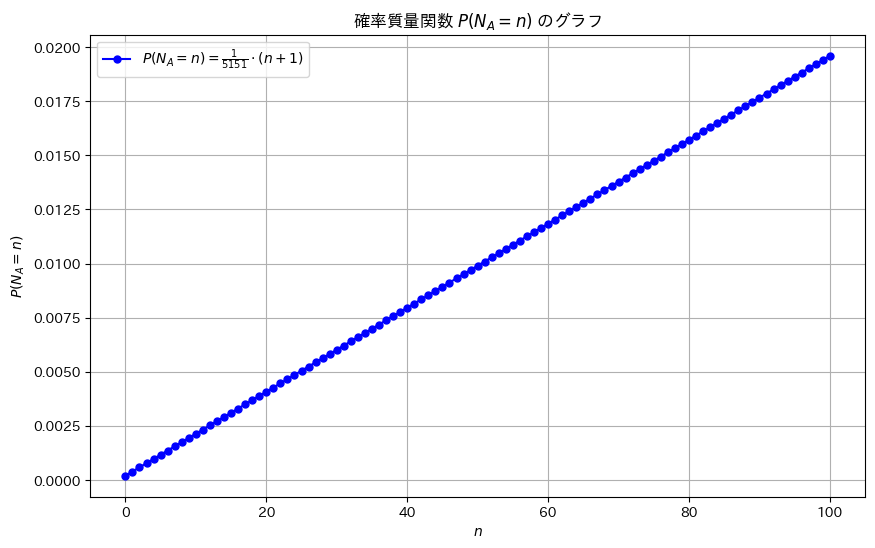
P(N_A = n)のプロット
# 2021 Q2(3) 2024.8.23
import matplotlib.pyplot as plt
import numpy as np
# 正規化定数 C
C_value = 1 / 5151
# n の範囲
n_values = np.arange(0, 101)
# 確率質量関数 P(N_A = n)
pmf_values = C_value * (n_values + 1)
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(n_values, pmf_values, 'bo-', label=r'$P(N_A = n) = \frac{1}{5151} \cdot (n + 1)$', markersize=5)
plt.xlabel(r'$n$')
plt.ylabel(r'$P(N_A = n)$')
plt.title(r'確率質量関数 $P(N_A = n)$ のグラフ')
plt.grid(True)
plt.legend()
plt.show()