超幾何分布の当たりの数の推定値を尤度比を使って求めました。

コード
シミュレーションによる計算
# 2021 Q2(2) 2024.8.22
import numpy as np
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# L(N_A + 1) / L(N_A) を計算し、条件を満たす最小の N_A を探索
# max(0, N_A - 85) ≤ 4 ≤ min(15, N_A) の式に基づき、取り出した豆Aが4粒の場合の N_A の範囲を設定 (4 ≤ N_A ≤ 89)
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
NA_optimal = NA_values[np.where(np.array(ratios) < 1)[0][0]]
print(f"L(N_A + 1) / L(N_A) < 1 となる最小の N_A は {NA_optimal} です。")
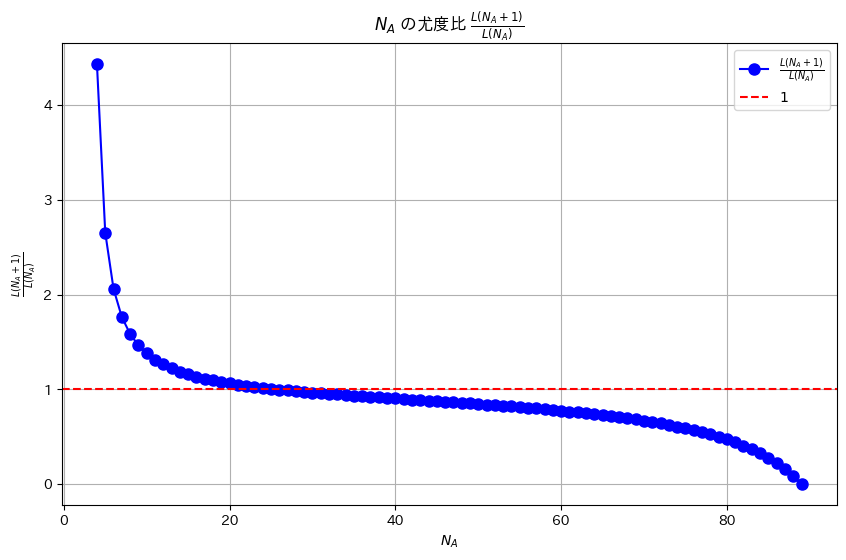
L(N_A + 1) / L(N_A) < 1 となる最小の N_A は 26 です。プロット
# 2021 Q2(2) 2024.8.22
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# N_A の範囲を設定
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(NA_values, ratios, 'bo-', label=r'$\frac{L(N_A + 1)}{L(N_A)}$', markersize=8)
plt.axhline(y=1, color='red', linestyle='--', label=r'$1$')
plt.xlabel(r'$N_A$')
plt.ylabel(r'$\frac{L(N_A + 1)}{L(N_A)}$')
plt.title(r'$N_A$ の尤度比 $\frac{L(N_A + 1)}{L(N_A)}$')
plt.legend()
plt.grid(True)
plt.show()
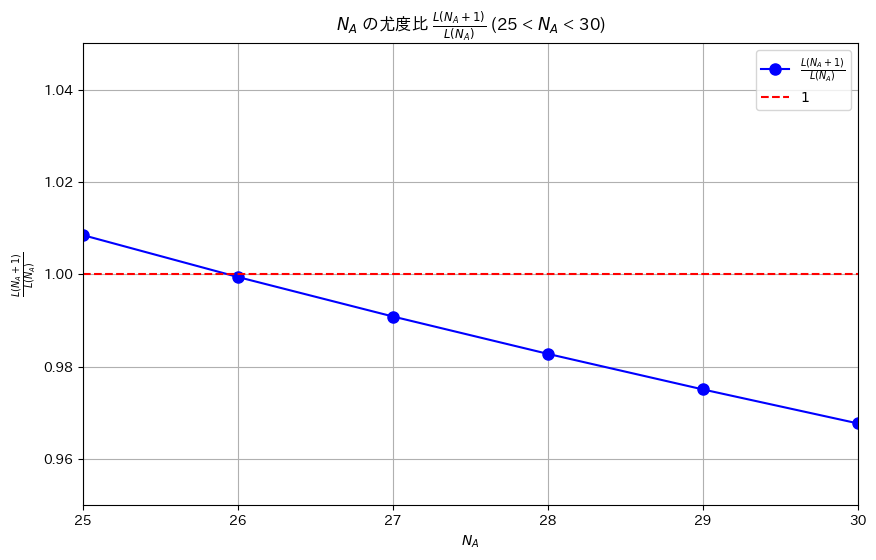
プロット(NA=26付近をズーム)
# 2021 Q2(2) 2024.8.22
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# N_A の範囲を設定
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
# 26付近のズームしたグラフを描画
plt.figure(figsize=(10, 6))
plt.plot(NA_values, ratios, 'bo-', label=r'$\frac{L(N_A + 1)}{L(N_A)}$', markersize=8)
plt.axhline(y=1, color='red', linestyle='--', label=r'$1$')
plt.xlabel(r'$N_A$')
plt.ylabel(r'$\frac{L(N_A + 1)}{L(N_A)}$')
plt.title(r'$N_A$ の尤度比 $\frac{L(N_A + 1)}{L(N_A)}$ (25 < $N_A$ < 30)')
plt.xlim(25, 30) # N_A = 26 付近をズーム
plt.ylim(0.95, 1.05) # y軸もズームして見やすく
plt.legend()
plt.grid(True)
plt.show()